電験三種 R1年 機械 問15 問題と解説

　問 題　　　　　

並行運転しているA及びBの2台の三相同期発電機がある。それぞれの発電機の負荷分担が同じ7300kWであり、端子電圧が6600Vのとき、三相同期発電機Aの負荷電流I_Aが1000A、三相同期発電機Bの負荷電流I_Bが800Aであった。

損失は無視できるものとして、次の(a)及び(b)の問に答えよ。

(a)　三相同期発電機Aの力率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 48
2. 64
3. 67
4. 77
5. 80

(b)　2台の発電機の合計の負荷が調整の前後で変わらずに一定に保たれているものとして、この状態から三相同期発電機A及びBの励磁及び駆動機の出力を調整し、三相同期発電機Aの負荷電流は調整前と同じ1000Aとし、力率は100%とした。

このときの三相同期発電機Bの力率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、端子電圧は変わらないものとする。

1. 22
2. 50
3. 71
4. 87
5. 100

 

 

 

 

 

　解 説　　　　

(a)

問題文に記載されている条件を図示すると、次のような等価回路を描くことができます。

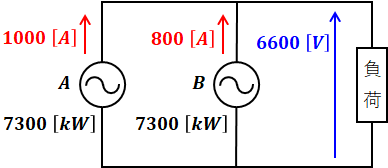
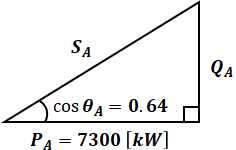
ここで、この同期発電機は三相なので、三相同期発電機Aの有効電力P_Aは次の式で表されます。

上式に等価回路に書き込んだ各種の値を代入すると、力率θ_Aを求めることができます。

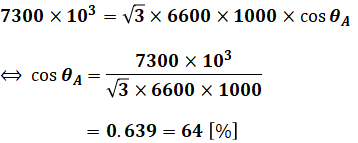
よって、正解は(2)となります。

(b)

問われているのは力率なので、(a)と同様の計算式を使いたくなるかもしれませんが、調整後の発電機Bを流れる電流の値がわからないので、この式からのアプローチは難しいです。

一方、力率は「(有効電力)/(皮相電力)」でも表すことができます。今回は、この式を解くこと目標に進めていきます。

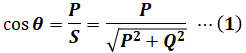
• 力率　　：cosθ
• 皮相電力：S [W]
• 有効電力：P [W]
• 無効電力：Q [W]

なお、発電機A、B、合計の区別、調整の前後の区別を付けるため、ここでは以下に示すようなマークを付けて解説していきます(以下は有効電力の例)。

• P_A：調整前の発電機A
• P_B：調整前の発電機B
• P_AB ：調整前の発電機AとBの合計
• P’_A  ：調整後の発電機A
• P’_B  ：調整後の発電機B
• P’_AB：調整後の発電機AとBの合計

よって、今回は調整後の発電機Bの力率が問われているので、これを(1)式に適用すると、以下の(2)式のように表すことができます。

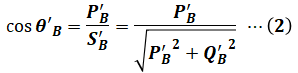
θ’_Bを算出するには、上式を見てもわかるように、P’_BとQ’_Bを求める必要があります。そこで、まずはP’_Bについて考えます。

調整前の負荷は各7300[kW]なので、負荷の合計P_ABは7300×2＝14600[kW]です。よって、調整後の負荷の合計P’_ABも14600[kW]となります。

ここで、調整後の発電機Aを流れる電流は1000[A]、電圧は6600[V]、力率100[%]より、有効電力P’_Aは次のように計算できます。

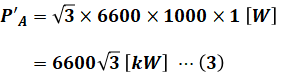
よって、調整後の発電機Bの有効電力P’_Bは以下のように算出されます。

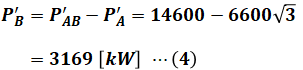
続いて、Q’_Bについて考えます。

これは調整前のQ_A＋Q_Bが調整後のQ’_A＋Q’_Bと同じ値になることから、等式を立てて差し引きで計算します。つまり、そのためにはQ_A、Q_B、Q’_Aの値を求める必要があります。

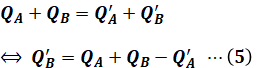
Q_Aについては(a)の計算結果を利用して、以下のように計算します。

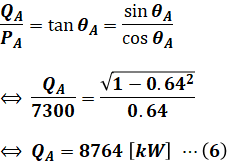
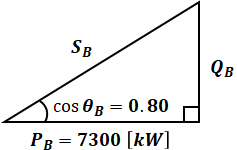
Q_BについてもQ_Aと同様に、力率cosθ_Bを求めてから三角比の計算で導出します。

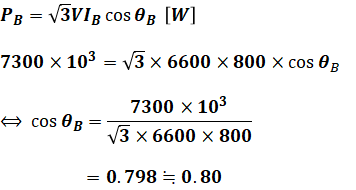
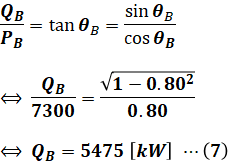
Q’_Aについては簡単です。調整後の発電機Aの力率は100[%]なので、計算するまでもなく無効電力は0となることがわかります。

(6)式、(7)式、(8)式で求めたQ_A、Q_B、Q’_Aの値を(5)式に代入すれば、Q’_Bの値を計算できます。

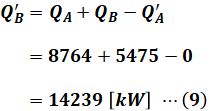
以上より、(4)式でP’_Bが、(9)式でQ’_Bがわかったので、これを(2)式に代入することで、問われている力率θ’_Bを算出することができます。

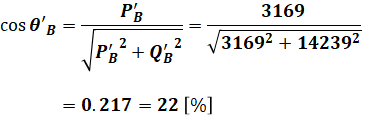
よって、正解は(1)です。