電験三種 R1年 機械 問14 問題と解説

　問 題　　　　　

2進数AとBがある。それらの和がA+B=(101010)₂、差がA-B=(1100)₂であるとき、Bの値として、正しいものを次の(1)～(5)のうちから一つ選べ。

1. (1110)₂
2. (1111)₂
3. (10011)₂
4. (10101)₂
5. (11110)₂

 

 

 

 

 

　解 説　　　　

AとBの和と差が2進数で与えられていますが、まずはこれらを馴染みのある10進数に変換します。

和である(101010)₂を10進数に直す際には、2進数の一の位が2の0乗、十の位が2の1乗、百の位が2の2乗…と対応していきます。つまり、以下の図のように書くことができます。

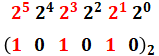
よって、これを計算すると、次の通りとなります。

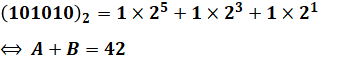
差である(1100)₂についても同様に計算します。

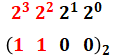
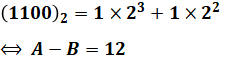
以上から、A＋B＝42とA－B＝12の連立方程式を解くことで、A＝27、B＝15と計算することができます。求めたいのはBの値を2進数で表したものなので、今度は15を2進数に変換します。

10進数を2進数にするには、以下のように元の数字(10進数の数値)を2でどんどん割っていって、その余りを下から上へ読んでいったものが答えとなります。

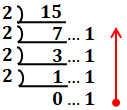
よって、(15)₁₀=(1111)₂だとわかります。

以上から、正解は(2)となります。