問 題
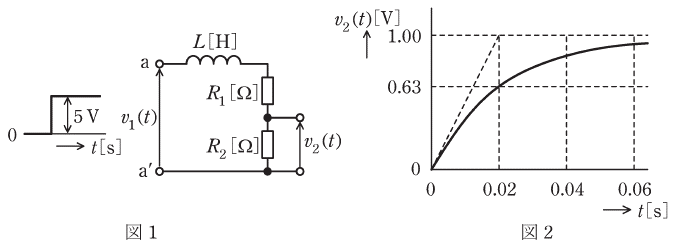
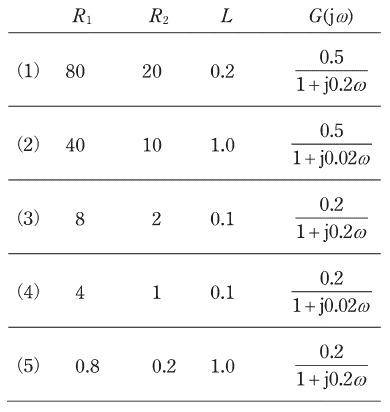
図1に示すR-L回路において、端子a-a’間に5Vの階段状のステップ電圧v1(t)[V]を加えたとき、抵抗R2[Ω]に発生する電圧をv2(t)[V]とすると、v2(t)は図2のようになった。
この回路のR1[Ω]、R2[Ω]及びL[H]の値と、入力をv1(t)、出力をv2(t)としたときの周波数伝達関数G(jω)の式として、正しいものを次の(1)~(5)のうちから一つ選べ。
解 説
選択肢の順番はR1、R2、L、G(jω)と並んでいるので、この順に解きたくなりますが、図2よりR2の端子間電圧が最終的に1[V]、するとR1の端子間電圧は5-1=4[V]ということがわかるだけで、電流は不明のためこれ以上計算が進みません。
よって、とりあえずR1、R2、Lのことは置いておいて、G(jω)について考えます。
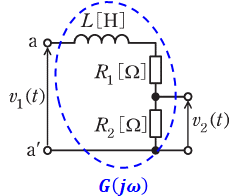
問題文より、入力をv1(t)、出力をv2(t)としたときの周波数伝達関数がG(jω)とあるので、これら3つの関係式は次のように表すことができます。
![]()
ここで、R1、R2、Lは直列に並んでいるので、この回路に流れる電流をIとすると、v1、v2は次のように表すことができます。
![]()
![]()
(2)式と(3)式を(1)式に代入すると、次のようになります。
![]()
ここで、解説の冒頭でも書きましたが、図2より充分に時間が経ったあとのR2の端子間電圧v2は1[V]なので、R1の端子間電圧は5-1=4[V]となります。両者の抵抗を流れる電流は同じなので電圧比はそのまま抵抗比とわかり、「R1=4R2」が成り立ちます。
よって、(4)式は次のように変換できます。
![]()
R1とR2の関係式はわかったので、今度はこれらとLの関係式について考えます。
図2でv2(t)=0.63とv2(t)=1.00のところが表記されています。ここでv2(t)=0.63が強調されているのは、電圧が立ち上がってから最大(定常状態)電圧の約63.2%になるまでに掛かった時間を「時定数」と定めているからです。
RL直列回路における時定数τの式は、以下のように表すことができます。
![]()
今回の場合、図2よりτ=0.02と読み取れます。また、RというのはここではR1とR2の和なので、R1+R2=4R2+R2=5R2として計算します。
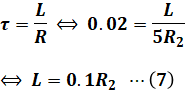
続いて、(7)式を(5)式に代入します。
![]()
上式をR2で約分し、その後、選択肢に合わせて右辺の左下を「1」にするため、分母分子を5で割ります。
![]()
(9)式と選択肢のG(jω)で一致するものが選択肢(4)しかないため、これが正解となります。
以上で正解は選べましたが、R1、R2、Lの値は算出できていません。これらはラプラス変換を使うことで導出することができます。
しかし、電験三種試験の出題傾向を見ると、ラプラス変換を知らないと解けない問題というのは近年出題されていません。そのため、試験対策という趣旨から離れてしまうので、ここではR1、R2、Lを求める解説は省略します。
もし興味がある場合には、「伝達関数 ラプラス変換」などのキーワードを元に、ご自分で調べてみてください。

コメント