問 題
次の文章は、星形結線の円筒形三相同期電動機の入力、出力、トルクに関する記述である。
この三相同期電動機の1相分の誘導起電力E[V]、電圧V[V]、電流I[A]、VとIの位相差をθ[rad]としたときの1相分の入力Pi[W]は次式で表される。
![]()
また、EとVの位相差をδ[rad]とすると、1相分の出力Po[W]は次式で表される。EとVの位相差δは( ア )といわれる。
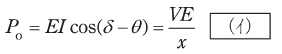
ここでx[Ω]は同期リアクタンスであり、電機子巻線抵抗は無視できるものとする。
この三相同期電動機の全出力をP[W]、同期速度をns[min-1]とすると、トルクT[N・m]とPの関係は次式で表される。
![]()
これから、Tは次式のようになる。
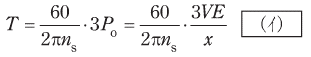
以上のことから、0≦δ≦π/2の範囲においてδが( ウ )なるに従ってTは( エ )なり、理論上π/2[rad]のとき( オ )となる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
- (ア) (イ) (ウ) (エ) (オ)
- 負荷角 cosδ 大きく 大きく 最大値
- 力率角 cosδ 大きく 小さく 最小値
- 力率角 sinδ 小さく 小さく 最小値
- 負荷角 sinδ 大きく 大きく 最大値
- 負荷角 cosδ 小さく 小さく 最大値
解 説
( ア )には「負荷角」か「力率角」が入りますが、力率角はその言葉からもわかるように、電力Pに関係する角度θで、電圧Vと電流Iの間の角度を指します(P=VIcosθ)。
一方の負荷角は、内部誘導起電力Eと電機子端子電圧Vの位相差で、δの記号で表されることが多いです。
よって、( ア )には「負荷角」が入ります。
( イ )に関して、三相同期電動機の出力は以下のように表すことができます。これはベクトル図を描いて導出することもできますが、頻出事項なので重要公式として覚えてしまったほうが便利だと思います。
![]()
- P:三相同期機の出力[W]
- Eo:内部誘導起電力[V](相電圧実効値)
- V:電機子端子電圧[V](相電圧実効値)
- X:同期リアクタンス[Ω]
- δ:EoとVとの位相角[rad]
なお、上式の3は三相の3なので、もし同期機全体ではなく1相あたりの出力が知りたければ、この3を抜けばよいです。今回の問題は1相分の出力Poが問われているため、係数の3は除いて考えます。
よって、( イ )には「sinδ」が入ります。
( イ )の答えがsinδだとわかれば、( ウ )、( エ )、( オ )に関しては比較的簡単に答えることができます。
「0≦δ≦π/2」はラジアンの表記ですが、度数に直すと「0°≦δ≦90°」となります。この範囲でサインカーブの軌跡を考えると、δ=0のときにsinδ=0で、ここからδが上がるとともにsinδも上がっていき、δ=90°でsinδは最大値の1をとります。
よって、( ウ )には「大きく」が入り、Tはsinδに比例するため、( エ )にも「大きく」が入ります。また、( オ )は「最大値」とするのが適切です。
以上から、正解は(4)となります。

コメント