電験三種 R1年 機械 問3 問題と解説

　問 題　　　　　

4極の三相誘導電動機が60Hzの電源に接続され、出力5.75kW、回転速度1656min^-1で運転されている。このとき、一次銅損、二次銅損及び鉄損の三つの損失の値が等しかった。このときの誘導電動機の効率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、その他の損失は無視できるものとする。

1. 76.0
2. 77.8
3. 79.3
4. 80.6
5. 88.5

 

 

 

 

 

　解 説　　　　

誘導電動機の効率を求める問題なので、入力に対する出力の比を答えればよいことになります。とはいえ、今回は入力に関する条件が一切書かれていません。しかし、出力と各種の損失を合わせたものが入力と同等となるため、以下のような式が成り立ちます。

上式のうち、出力はすでに問題文で5.75[kW]と与えられています。また、損失は一次銅損、二次銅損、鉄損の3種類がありますが、問題文よりこれらは全て同じ値になるので、どれか一つを求めれば3倍するだけで損失の合計が求められます。

ここで、誘導機の二次銅損に関する重要な式があります。次に示す、誘導機の「二次入力：二次銅損：出力」の関係式を使う機会は多いので、ぜひ押さえておいてください。

• P_m：機械出力 [W]
• P₂：二次入力 [W]
• P_c2：二次銅損 [W]
• s：滑り

これを図にまとめると、次のようになります。

上式のうち、出力P_mは既知の値なので、滑りsの値さえわかれば二次入力P₂の値がわかり、さらにそこから二次銅損P_c2が計算できます。よって、次にやることは滑りsの値を考えることです。

誘導機の滑りsは以下に示す計算式で定義されます。これも重要公式として、必ず押さえておきたい式のひとつです。

• s：滑り
• N_s：同期速度(回転磁界の速度) [min^-1]
• N：回転速度(回転子の速度) [min^-1]

上式を解くためには同期速度N_sと回転速度Nの値が必要です。回転速度Nは問題文で1656min^-1とあり、同期速度N_sについては次の式から計算することができます。

• N_s：同期速度 [min^-1]
• p：磁極の数 [極]
• f：周波数 [Hz]

これで正解を求めるために必要な式が揃ったので、あとは問題文で与えられた式を代入して、どんどん計算していきます。

まず、同期速度N_sについては次のようになります。

続いて、滑りsを算出します。

次に求めるのは、二次入力P₂です。

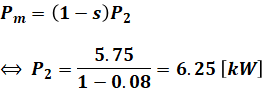
よって、二次銅損P_c2は次のように計算できます。

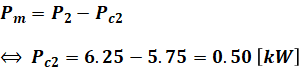
以上から二次銅損P_c2＝0.50[kW]とわかったので、一次銅損も鉄損も0.50[kW]となり、以下の式のように効率ηを求めることができます。

よって、正解は(3)となります。