電験三種 R1年 法規 問12 問題と解説

　問題　　　　　

三相3線式の高圧電路に300kW、遅れ力率0.6の三相負荷が接続されている。この負荷と並列に進相コンデンサ設備を接続して力率改善を行うものとする。

進相コンデンサ設備は図に示すように直列リアクトル付三相コンデンサとし、直列リアクトルSRのリアクタンスX_L[Ω]は、三相コンデンサSCのリアクタンスX_C[Ω]の6%とするとき、次の(a)及び(b)の問に答えよ。

ただし、高圧電路の線間電圧は6600Vとし、無効電力によって電圧は変動しないものとする。

(a)　進相コンデンサ設備を高圧電路に接続したときに三相コンデンサSCの端子電圧の値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(b)　進相コンデンサ設備を負荷と並列に接続し、力率を遅れ0.6から遅れ0.8に改善した。このとき、この設備の三相コンデンサSCの容量の値[kvar]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

正解 (a)-(5), (b)-(3)

　解説　　　　

三相3線式の電路に対して、三相負荷と進相コンデンサ設備が並列に接続されているので、この三相回路の1相あたりの等価回路は以下のように描くことができます。

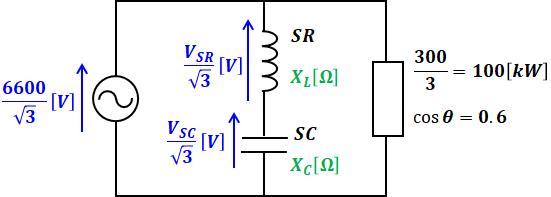
直列リアクトルSRの端子間電圧をV_SR[V]、三相コンデンサSCの端子間電圧をV_SC[V]とすると、1相あたりの電圧は上図のようにそれぞれV_SR/√3[V]、V_SC/√3[V]となります。

(a)ではSCの端子間電圧が問われていますが、電流が一定ならオームの法則により電圧と抵抗は比例するため、次のような計算式が成り立ちます。

ここで、(V_SR/√3＋V_SC/√3)＝6600/√3、問題文よりX_L＝0.06X_Cなので、上式は次のように計算を進めることができます。

以上から、正解は(5)となります。

進相コンデンサ設備を接続する前は負荷の遅れ力率が0.6なので、有効電力[kW]・無効電力[kvar]・皮相電力[kV・A]は次のようになります。

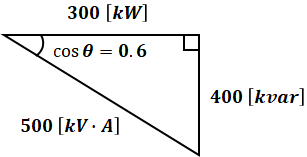
ちなみに、上図のうち400[kvar]、500[kV・A]は三角比(cosθ＝斜辺/横辺)や三平方の定理から求めることができます。

ここに進相コンデンサ設備を入れると遅れ力率が0.8に改善したということなので、これを図示すると次のようなイメージとなります。

上図では、進相コンデンサ設備が無効電力に影響を与える容量の大きさをQ[kvar]としています。進相コンデンサ設備に抵抗があるわけではないので、有効電力には影響を与えず300[kW]のままです。

これにより無効電力が400から(400－Q)に変化した結果、cosθが0.6から0.8に変化しています。

上図の実線部分だけを改めて以下に記載します。また、斜辺の容量は三平方の定理を用いると下図のように表すことができます。

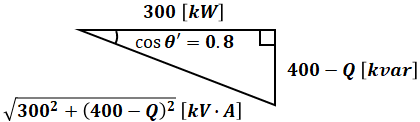
上図より、次に示すような三角比の計算によってQの値を求めることができます。

ただし、ここで算出したQ＝175[kvar]というのは、進相コンデンサ設備全体(SRとSCの合計)の容量です。今回問われているのはSCだけの容量なので、これを考慮する必要があります。

X_L＝0.06X_Cであり、SRの容量Q_LとSCの容量Q_Cのベクトルは反対向き(遅れと進み)なので、次のように計算することによって、問われているSCの容量Q_Cを求めることができます。

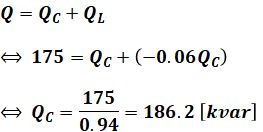
以上から、正解は(3)となります。

電験三種 R1年法規問12 問題と解説