電磁誘導は、コイルの中を通過する磁束の量が変化すると誘導起電力が生じてコイルに電流が流れるという現象でした。一方、コイルに電流が流れていてその電流に変化があった場合も、磁束の量が変化するので、やはり誘導起電力を生じます。
このようにコイル自身を流れる電流の変化で磁束も変化し、誘導起電力を生み出す作用のことを自己誘導作用といいます。また、この起電力のことを自己誘導起電力といい、その大きさは次の式で表すことができます。
![]()
- E:誘導起電力 [V]
- N:巻数
- ΔΦ:磁束の増加分 [Wb]
- Δt:時間 [s]
- L:自己インダクタンス [H]
- ΔI:電流の変化量 [A]
上式のうち左側は、前項で扱った電磁誘導の際の誘導起電力の式と全く一緒です。また、右側は自己誘導起電力特有の式になりますが、重要式なので公式として覚えておいてください。
インダクタンスLはコイルの性能を表すパラメータですが、特に自己誘導作用でのインダクタンスのことを自己インダクタンスといいます。単位は[H]と書いて「ヘンリー」と読みます。自己インダクタンスは以下の式で表すことができます。
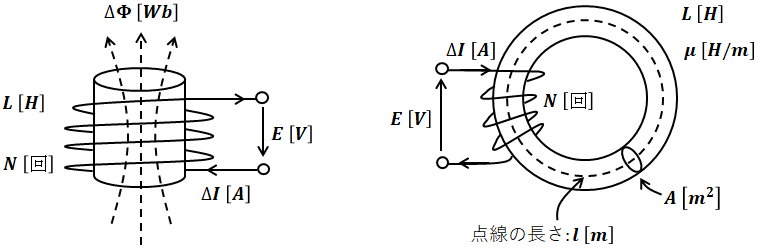
![]()
- L:自己インダクタンス [H]
- N:巻数
- Φ:磁束 [Wb]
- I:電流 [A]
- μ:環状鉄心の透磁率 [H/m]
- A:環状鉄心の断面積 [m2]
- l(エル):磁路の長さ [m]
自己インダクタンスLが上式の2項目で表されるというのは、上で紹介した自己誘導起電力Eの公式における2項目と3項目を等式でつないで、Lについて解けば導くことができます。
一方、Lを上式第3項(μ、A、N、lを使う式)で表しているほうは、環状コイルでよく使われる表現です(第2項のN、Φ、Iを使う式のほうは、まっすぐのコイルでも環状コイルでも使える式です)。
環状コイルにおいてなぜ上式のように表せるかという理由については以下で説明しますが、これは導出過程を理解するよりも、公式として暗記してしまったほうが早いかもしれません。導出過程よりも各種パラメータの関係(LはNの2乗に比例する…など)が大事なので、ぜひ上式は押さえてください。
(以下は参考までに。上式を公式として覚える場合は、以下のことは抑えなくても大丈夫だと思います。)
自己インダクタンスの基本式は次の通りです。
![]()
ここで、磁束Φ[Wb]は起磁力F[A]を磁気抵抗R[A/Wb]で割ったものとなりますが、そのそれぞれは次のように表されます(以下の等式については磁気回路のページで詳しく解説します)。
![]()
![]()
![]()
(1)式に(2)式を代入し、さらに(3)式と(4)式を代入した上で計算を進めると、以下の通り上記で紹介した公式と同じ式が導けます。
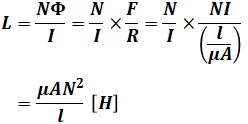

コメント