RLC直列回路についてはこちらのページで扱いましたが、その回路において、ある特定の周波数fr[Hz]のときに誘導性リアクタンスXL[Ω]の大きさと容量性リアクタンスXC[Ω]の大きさが等しくなります。これら2つのリアクタンスは位相が真逆(XLはπ/2の遅れで、XCはπ/2の進み)なので、その作用は互いに打ち消し合います。
両者のリアクタンスXの大きさが一緒のとき、RLCのうちLとCが完全に打ち消されるので、結果としてRのみの回路と見なせます。このように、XL=XCによって回路のインピーダンスZが小さくなり、大きな電流が流れるようになる現象を直列共振といい、このときの周波数fr[Hz]をその回路の共振周波数といいます。
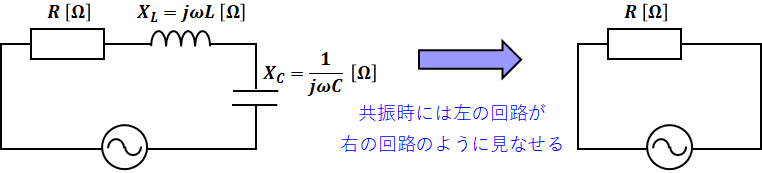
上図において、インピーダンスZは次式で表されます。
![]()
上式のうち虚数部(コイルとコンデンサの部分)をまとめると、次のように変換できます。

ここで、インピーダンスZが最も小さくなる(回路に流れる電流が大きくなる)のは、虚数部が0のときなので、共振周波数fr[Hz]は次のように計算することができます。
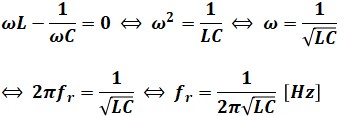
ちなみに、このときのインピーダンスZは、虚数部がなくなるので、Z=Rとなります。
共振周波数frを求める上式は重要なので、ぜひ覚えておいてください。長くて覚えるのが大変…という方は、直列共振の条件式として、せめて以下の関係式だけでも押さえておいてください。これさえ覚えておけば、あとは試験中に計算を進めても大して時間は掛からないと思います。
![]()

コメント