RLC並列共振回路

前項で扱ったRLC直列回路の共振の条件は、以下の式で表すことができました。

または

(上の2つの式は全く同じ意味です。どちらかだけ押さえておけば充分です。)

同様に、RLC並列回路においても全く同じ条件式(上式)で共振が起こります。ただし、直列回路と並列回路では異なる点もありますので、この項では、並列共振を直列共振と比較しながら解説していきます。もしRLC直列回路について理解が曖昧な場合は、先に前項を読んで確認しておいてください。

まず、RLC直列回路では、共振周波数f_r[Hz]のときに誘導性リアクタンスX_L[Ω]の大きさと容量性リアクタンスX_C[Ω]の大きさが等しくなり、これらの作用が打ち消し合うことで、LもCも短絡してRだけの回路のように見なすことができました。

一方、RLC並列回路でも、誘導性リアクタンスX_L[Ω]の大きさと容量性リアクタンスX_C[Ω]の大きさが等しくなるような周波数が共振周波数f_r[Hz]となります(だから、最初で紹介した式は直列でも並列でも共通となります)。

ここで、並列回路の性質から、RLC並列回路でのコイルとコンデンサの端子電圧の大きさは等しく、上記のようにリアクタンスの大きさが等しい場合(ただし誘導性リアクタンスと容量性リアクタンスの位相は反対)、両者(コイルとコンデンサ)を流れる電流の大きさは一緒で、向きは逆ということになります。

…ということは、下図左側の電気回路において、コイルとコンデンサのみの閉回路をぐるぐる電流が流れているということです。つまり、電源側から見れば、電流がコイルやコンデンサ側に流れる余地はなく、これら(コイルとコンデンサ)の合成リアクタンスは無限大であると見なすことができます。

よって、下図左側の電気回路において、電源や抵抗を含む左半分の閉回路と、コイルやコンデンサを含む右半分の閉回路を切り離して考えることができるので、電源を流れる電流は抵抗にしか流れず、下図左側は右側のように描き換えることができます。

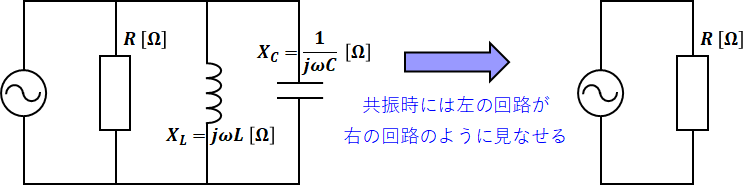
つまり、直列共振のときは短絡させることのできたLやCが、並列共振では開放させることになります。共振周波数f_rの式も一緒で、LやCが消えることも同じですが、短絡となるか開放となるかについては注意してください。

ちなみに、以上から、並列共振のときも直列共振と同様、回路全体のインピーダンスZは、Z=Rとなります。ただし、Z=RとなったときのZが大きい値なのか小さい値なのかという点に関して、直列共振と並列共振とでは意味合いが異なります。

直列共振のときにはX_LとX_Cが打ち消し合うことでインピーダンスZが最小になるので、電源を流れる電流Iは最大になります。

一方、並列回路では並列に並ぶものが増えるほど合成インピーダンスが下がる傾向にあるので、並列共振によってX_LとX_Cが打ち消し合うと、逆にインピーダンスZは最大になります。そのため、この場合、電源を流れる電流Iは最小になります。