RLC並列回路とは、交流回路の3つの素子(抵抗、コイル、コンデンサ)が並列に並んだ回路のことです。
2つの素子でRL並列回路、RC並列回路、LC並列回路を構成することもありますが、直列回路のときと同様、RLC並列回路さえをしっかり理解しておけばほかのパターンでも対応できるため、個々に分けて覚える必要はありません。
RLC並列回路の回路図は以下のように描かれます。
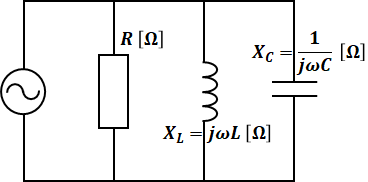
回路全体のインピーダンスZは、並列なので、個々の素子の逆数の和が、Zの逆数となります。
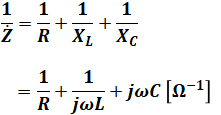
上式の形さえ覚えておけばよく、実際の試験問題で各数値が与えられている場合は、上式に数値を代入してからこの先の計算をしたほうが簡単な場合が多いと思います。
ここでは一般論として説明するので、上式のまま、Z=~の形に直すと、次のように計算を進めることができます(以下の過程はひとつひとつ覚えようとしなくて大丈夫です。参考までに確認してください)。
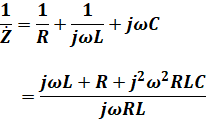
ここで、j2=-1なので、
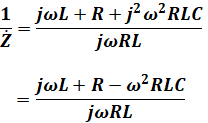
となり、分母・分子に「j」を掛けて分母を実数にするとともに、分子の実数部と虚数部に分けると、
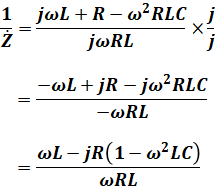
と計算することができます。よって、回路全体のインピーダンスZは、
![]()
と表すことができます。この段階でもまだ分母に「j」があるので、これを解消したい場合は、分母・分子に「ωL+jR(1-ω2LC)」を掛けて計算をさらに進める必要があります。試験においてインピーダンスZの大きさが聞かれた場合、分母の「j」を消した上で、実数部と虚数部に分けて、それから三平方の定理を使って計算しなくてはいけません。
けれど、もしそのような出題があった場合、この流れで計算を進めるよりも、冒頭でも書いたように問題文で与えられた数値を先に代入したほうが遥かに計算が簡単になる場合が多いです(そのため、ここでは、上式以降の計算は割愛します)。
以上、やや複雑な話を含めて色々と説明をしてきましたが…この項で大切なことは、最初の式ひとつのみです。強調のため、もう一度同じ式を以下に載せておきます。これだけ覚えておいてください。
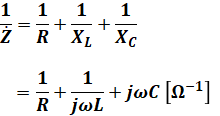
補足
また、参考書などによっては、並列回路の際にアドミタンスを使って説明しているものもあります。
アドミタンスの考え方を使えば計算問題が簡単になることもある一方で、中途半端な理解では逆に混乱の種にもなるため、個人的には、電験三種の試験において積極的にアドミタンスを使う必要はないと考えます(ただし、問題文自体が穴埋め形式になっていてアドミタンスを使うことが誘導されている場合などは別です)。
そこで、以下ではアドミタンスの基本について参考程度に軽く解説します。
インピーダンスZの逆数は、アドミタンスYで表すことができます。単位は[Ω]の逆数、つまり、[Ω-1]ですが、これは[S]と記されます(読み方はジーメンス)。
![]()
イメージとしては、電流の流れにくさを表すのがインピーダンスZなので、アドミタンスYは電流の流れやすさを表すパラメータということになります。
これを使えば、上記のようにインピーダンスZの逆数が、R、XL、XCそれぞれの逆数の和と等しい…という複雑な計算が、以下の式のような単純な和として計算できるようになるので、使い所によっては便利です(Yの右下にR、L、Cが付いたものは、それぞれの素子のアドミタンスです)。
![]()
ただし、もとのインピーダンスZを知りたければ、求めたアドミタンスYをまた逆数にしなければいけないなどの注意点もあり、計算を簡略化しようとした結果、計算ミスにつながるなどのリスクもあります。
そのため、もし混乱しそうな場合は、基本的にアドミタンスYの考え方は持ち出さなくても構わないと思います(電験三種の範囲の計算問題では、問題文で誘導されていない限り、Yを使わなくてもそこまで複雑な計算にならないはずです)。

コメント