前項では重ね合わせの原理のルールについて説明したので、この項では、具体的な例題を取り上げます。
例題
以下の電気回路において、各抵抗を流れる電流I1、I2、I3の値をそれぞれ計算してみてください。
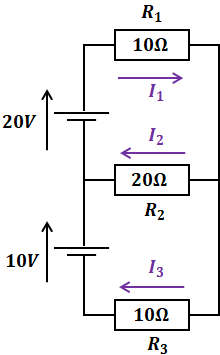
解説
キルヒホッフの法則を使っても解くことができますが、未知数が3つあるので、3式の連立方程式を解くことになり面倒です。そこで、この電気回路のように電源が2つある場合には、重ね合わせの原理が活用できることを思い出してください。
まずは20Vの電源だけ残して、10Vの電源はないものとして(短絡させて)考えます。
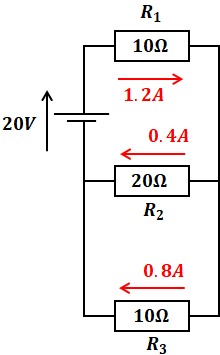
すると、電気回路は上図のようになります(この時点では赤字はまだ未知数です)。よって、3つの抵抗の合成抵抗Rを計算することができます(R2とR3が並列で、それとR1が直列)。
![]()
上式から回路全体を流れる電流I(=I1)は
![]()
となり、I2とI3は、I1の1.2Aを1:2(抵抗値の逆数)に分けるので、I2=0.4、I3=0.8となります(以上から、上図の赤字を書き込むことができます)。
続いて、今度は反対に10Vの電源だけ残して、20Vの電源はないものとして(短絡させて)考えます。
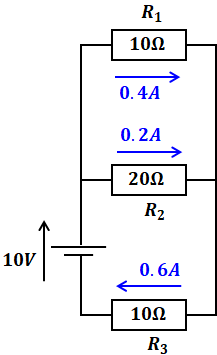
先ほどと同様に考えると、今度は3つの抵抗の合成抵抗Rが、R1とR2が並列で、それとR3が直列になります。よって、次のように計算することができます。
![]()
![]()
また、I1とI2は、I3の0.6Aを2:1(抵抗値の逆数)に分けるので、I1=0.4、I2=0.2となります(以上で、上図の青字を書き込むことができます)。
上記の2つの電気回路を合わせると(赤字の電流値と青字の電流値の和を計算すると)、もとの電気回路において、各抵抗を流れる電流I1、I2、I3の値を求めることができます。
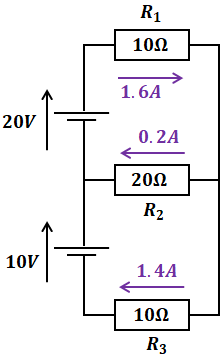
重ね合わせの原理は、このように電源が複数ある場合の計算問題で使うと、計算が簡略化されるので有益です。

コメント