インダクタンスと静電容量の位相

前項では、インダクタンスL[H]と静電容量C[F]の最も基本的な部分を説明しました。電気回路においてはこれらを[Ω]の単位に直さなければ計算ができないので、以下の式のように、それぞれコイルのリアクタンスX_L[Ω]とコンデンサのリアクタンスX_C[Ω]に変換できます。

前項ではここまでの説明にとどめましたが、実際には、上記のリアクタンスには位相があります。位相とは、周期的な動きをするものが、ある周期のうち、今どの点に存在しているかを示す変数です。

時間変化による周期はサインカーブを描くことが多いので、周期は2π[rad](360°)を1周期とすることが普通です。よって、位相の単位は[rad](ラジアン)または[°](度)となります。

上記の説明では結局位相が何なのかよくわからないかもしれません。…が、電験三種の試験対策としてはここを掘り下げる必要はありません(興味があれば別途調べてみてください)。むしろ大事なことは、以下の2点を押さえておくことです。

1点目について、位相には向きがあるということはベクトルで表すことができるということです。位相を持った数値同士の足し算や引き算は単純な和や差にはならず、ベクトル和で考える必要があります。

2点目について、交流回路では電圧が絶え間なく変動していますが、それに合わせて電流も変動しています。位相差が0の場合は、電圧が上がれば電流も同時に上がり、電圧が下がれば電流も同時に下がります。

しかし、位相差がある場合には、電圧が上がって少し経ってから電流が上がり始める…といったことが起こります。今のところ、このような簡単な理解で構いませんが、より詳しくは正弦波交流の波形と位相のページで解説しています。

リアクタンスが持つ位相の大きさ(角度)について、まず、抵抗R[Ω]の位相は0[rad]=0[°]になります。これは、抵抗Rを流れる電流I_Rと電圧V_Rとの間に位相差がなく、電流I_Rと電圧V_Rの変動が一致しているということになります。

それに対して、コイルのリアクタンスX_L[Ω]の場合、コイルに流れる電流I_Lは電圧V_Lに対してπ/2[rad](90°)だけ遅れます。

遅れとは、基準ベクトルに対して時計回りに回転する方向を指す言葉です。電流の変化が、電圧の変動に対して遅れることからこのように呼んでいます。繰り返しますが、電流が電圧に対して遅れるという表現です。

一方、コンデンサのリアクタンスX_C[Ω]の場合、コンデンサに流れる電流I_Cは電圧V_Cに対してπ/2[rad](90°)だけ進みます。

進みとは、基準ベクトルに対して反時計回りに回転する方向を指す言葉です。電流の変化が、電圧の変動に対して進んでいることからこのように呼んでいます。繰り返しますが、電流が電圧に対して進んでいるという表現です。

これをベクトル図で表すと以下のようになります。赤矢印で示すベクトルは抵抗とコンデンサを持つ回路(RL回路)、青矢印で示すベクトルは抵抗とコンデンサを持つ回路(RC回路)の一例を示しています。

また、抵抗R、コイルのリアクタンスX_L、コンデンサのリアクタンスX_Cの位相は次のように描くことができます。

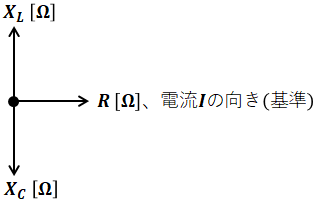
先ほどの図とはLとCの位置関係(上下)が反対になっていますが、これには理由があります。先ほどは電圧Vを基準にして電流が遅れているとか進んでいるとかいう話をしましたが、今回は電流Iを基準としています。

Vを基準にしてIを考えるときと、Iを基準にしてVを考えるときとでは、遅れや進みの関係は反対となります。また、オームの法則よりRやXとVは比例関係にあるため、結局、Iを基準にすれば、X_Lは90°の進み、X_Cは90°の遅れということになります。

…とはいえ、このあたりが複雑に感じる方は、最初から完璧に理解しようと思う必要はありません。大事なことは、RとXは位相が90°ずれていること、Xの中でもX_LとX_Cとでは位相が180°ずれていることの2つです。これらはしっかりと抑えておいてください。

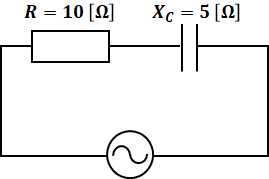
以上を踏まえて、たとえば抵抗Rが10[Ω]で、コンデンサのリアクタンスX_Cが5[Ω]の次の図のような電気回路があるとします。

その合成抵抗Z[Ω]は次のように計算できます(合成抵抗と書きましたが、正確には合成インピーダンスといいます。これについては次項で解説します)。計算方法は、直角三角形なので三平方の定理を使います。

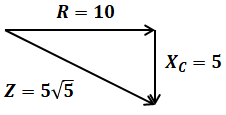
続いて、今度は抵抗もコイルもコンデンサもある場合を合成抵抗を考えます(ここも同様、正確には合成インピーダンスです。次項参照)。X_LとX_Cは位相が真逆(π[rad]のずれ)なので打ち消し合い、その差し引きと、Rとの合力を計算することになります。

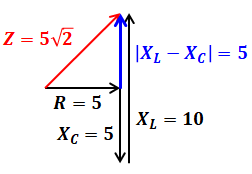
すると、上図のようにX_C=5と、それとは反対向きのX_L=10を合わせた結果、その差し引きはX_L側に5[Ω]となります。よって、合成抵抗(合成インピーダンス)は次のように計算することができます。

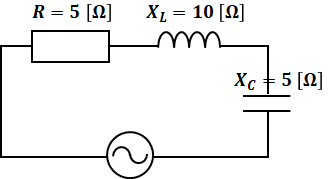
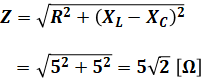
コメント