演算増幅器(オペアンプ)とは、半導体集積回路(IC)の一種で、回路図では以下のように表されます。
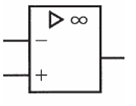
上図のうち、左側の2つが入力端子(-端子と+端子)であり、右側が出力端子です。2つの入力端子電圧の差のことを差動成分といいますが、演算増幅器は、その差動成分を高い利得で増幅する回路です(利得については以下で解説しますが、とりあえずは倍率のようなものと考えてください)。
演算増幅器の入力インピーダンスは極めて大きく、理想的な演算増幅器では入力インピーダンスが無限大だと考えます。上図において「▷∞」とあるのは、このことを示しています。入力インピーダンスが無限大なので、入力端子電流はほぼ0[A]とみなすことができます(抵抗が大きすぎて、電流が全く流れないということです)。
一方、演算増幅器の出力インピーダンスは非常に小さく、理想的には出力インピーダンスが0ということになります。すると、電流は損失なく流れることができるので、その出力端子電圧は負荷による影響を受けにくいです。
以上のような条件が揃えば、入力端子の差動成分に対する出力電圧の比である増幅度が無限大となります。つまり、理想的な演算増幅器とは、以下の3条件を満たす演算増幅器のことをいいます。
- 入力インピーダンスが無限大
- 増幅度が無限大
- 出力インピーダンスが0
ここで、この増幅器に抵抗などの部品を用いて負帰還をかけ、安定した有限の増幅度になるように調整すれば、入力電圧Vin[V]を何倍かした出力電圧Vout[V]を得ることができ、増幅器として利用できます(何倍になるかは、入力電圧や抵抗の大きさによって決まります)。
これを回路図で表すと、たとえば次のようになります。
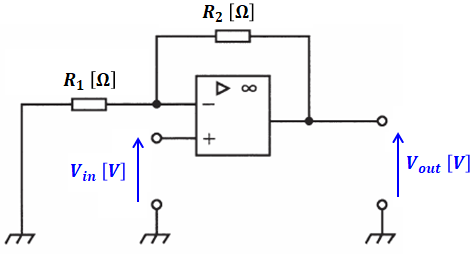
上図を用いた計算問題は頻出ですが、計算の進め方については次項で扱います。ちなみに、上図では入力電圧Vinを接地面と+端子との電圧差としていますが、-端子側に電圧を掛けて入力電圧Vinとする場合もあります。どちらの場合でも計算方法や解き方に違いがあるわけではないので、特に意識しなくても大丈夫です。
この項の最後に、上記回路の結果として得られる倍率の名称である「増幅度」と「電圧利得」について説明します。
増幅度とは、入力電圧Vin[V]に対する出力電圧Vout[V]の比のことをいいます。単位は「倍」または「単位なし」で表現することもあります。
ちなみに、先ほど理想的な演算増幅器の増幅度は無限大といいましたが、それは演算増幅器のみについての話です。ここで扱っている増幅度は、上図の電気回路全体で考えた出力と入力の比です。区別してください。
![]()
一方、似たような言葉に電圧利得があります。
電圧利得とは、入力電圧Vin[V]に対する出力電圧Vout[V]の比を以下の式に当てはめた数値です。こちらは単位が[dB]となります(デジベルと読みます)。
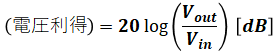
どちらも似たようなものですが、問題によって増幅度を聞いてきたり電圧利得を聞いてきたりするため、両方を区別して覚えておかないと、計算結果が選択肢と合わないというおそれがあるので注意してください。

コメント