電流が流れているとき、その周りには磁界が生じています。それは常に成り立つ事実ですが、電流の流れ方によって磁界の強さは変わってきます。電流のパターンは主に以下の4種類があるので、これらをそれぞれについて磁界の式を覚える必要があります。
- 直線導体
- 円形コイル
- ソレノイド
- 環状コイル
前項では「直線導体」と「円形コイル」を扱ったので、本項では「ソレノイド」と「環状コイル」の解説をします。
ソレノイドによる磁界
ソレノイドとは、螺旋状に巻いてあるようなコイルのことです。前項で円形コイルがN回巻きの場合を説明しましたが、円形コイルのN回巻きは、あくまで平面上でぐるぐるにしたイメージです。一方、こちらは立体的に(=螺旋状に)ぐるぐる巻きにしているイメージとなります。
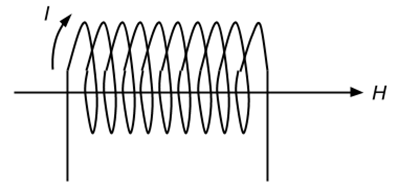
また、ソレノイドの長さは普通は当然有限ですが、試験問題においては無限長ソレノイドと表現されることが多いです。それは、無限長ソレノイドであれば端っこが存在しないため、計算が簡単になるからです。
無限長ソレノイドに流れる電流はコイルに沿って螺旋状に流れますが、ソレノイドの中心を通る磁界は、円形コイルのときと同様に直線となります(中心以外の部分を通る磁界は曲線になりますが、それでは計算問題が成立しないので、電験三種の試験では中心のみを扱います)。
このとき、ソレノイドを流れる電流がつくる磁界Hは、以下の式で表されます。
![]()
- H:磁界 [A/m]
- n:1mあたりの巻き数 [m-1]
- I:電流 [A]
問題によっては1mあたりの巻き数nが与えられていないときがありますが、そういうときは大体、全長と全巻き数が書いてあります。全巻き数を全長で割れば1mあたりの巻き数が出せますので、そのように対応してください(無限長の式なのに全長があるものに使うのは違和感かもしれませんが、充分な長さのあるコイルなら無限長と同じ計算式を使うことができます)。
環状コイルによる磁界
環状コイルは下図のような形状のコイルで、ソレノイドをぐるっと丸めたようなものです。
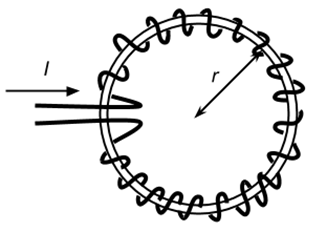
環状コイルの磁界で問題にされるのは、コイル内部の磁界です。つまり、上図の円の中心ではなく、コイルの内側のことを指していることに注意してください。ソレノイドの作る磁界がコイルの真ん中を通っていたのと同じ考え方です。
このとき、環状コイルを流れる電流がつくる磁界Hは、以下の式で表されます。
![]()
- H:磁界 [A/m]
- N:巻き数
- I:電流 [A]
- r:環状コイルの半径 [m]
以上、前項と合わせて4つの磁界の式は、公式としてぜひ押さえておいてください。

コメント