電流が流れているとき、その周りには磁界が生じています。それは常に成り立つ事実ですが、電流の流れ方によって磁界の強さは変わってきます。電流のパターンは主に以下の4種類があるので、これらをそれぞれについて磁界の式を覚える必要があります。
- 直線導体
- 円形コイル
- ソレノイド
- 環状コイル
この項では「直線導体」と「円形コイル」を、次の項では「ソレノイド」と「環状コイル」を扱います。
直線導体による磁界
直線導体とは、まっすぐな銅線(導体であれば銅線でなくても可)があるだけの状態です。ここに電流を流すと、その電流に応じた強さの磁界が銅線の周りに円を描くように発生します。

このとき、直線導体を流れる電流がつくる磁界Hは、以下の式で表されます。
![]()
- H:磁界 [A/m]
- I:電流 [A]
- r:導体と磁界の距離 [m]
磁界は、電流を円周で割った値となる、と覚えてください。導体から基準地点(測定地点)までの距離であるrが大きく(遠く)なればなるほど、当然磁界は弱くなっていきます。
また、磁界には向きがあります。上図の通り、電流が画面下から画面上に流れている場合、磁界の向きは(上から見て)反時計回りとなります。これは、右ねじの法則に従っています。
円形コイルによる磁界
上の例は電流がまっすぐで磁界が円を描いていましたが、円形コイルの場合はこれとは逆になります。つまり、円形コイルなので電流が円を描くように流れますが、そのとき、円の中心を通る磁界はまっすぐに伸びます(円の中心以外の部分を通る磁界は曲線になりますが、それでは計算問題が成立しないので、電験三種の試験では中心のみを扱います)。
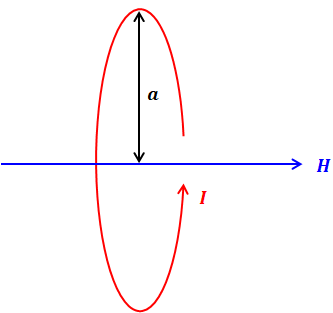
このとき、円形コイルを流れる電流がつくる磁界Hは、以下の式で表されます。
![]()
- H:磁界 [A/m]
- I:電流 [A]
- a:導体と中心の距離(円形コイルの半径) [m]
ここでも磁界の向きは右ねじの法則に従います。
また、ここでは上図のようにコイルが1巻きである場合を考えていますが、コイルは何重にも巻いてあることもあります。コイルの巻き数がNのとき、磁界の強さは単純にN倍になります。
![]()

コメント