磁界

前項は、2つの点磁極があるとその間には磁力が働くという話でした。そして、その磁力が働く空間のことを「磁界(磁場)」といいます。磁界の強さは数値化でき、その式は以下のように表すことができます。

• H：磁界[A/m]
• μ₀：真空の透磁率　4π×10^-7[H/m]
• m：磁荷(磁極の強さ)[Wb]
• r：磁極間の距離[m]

この式は、前項で扱った磁力の式に似ています。

(参考：磁力の式)

具体的には、2つの点磁極の一方を単位磁極(つまり1[Wb])としたときの磁力が、この「磁界」と等しくなります。よって、次の式が成り立ちます。

これは、磁界H[A/m]の空間にm[Wb]の磁極を置いたときの磁力F[N]を求める式となります。

また、磁界というのは目に見えなくてわかりづらいので、以下の図のように可視化することがあります。

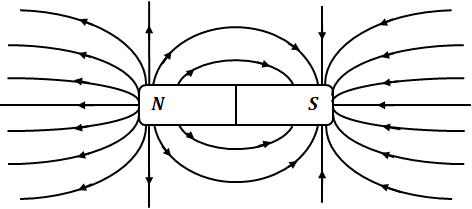
上図の矢印の通り、磁力はN極からS極へと向かう磁力線として描くことができます。磁力線は無数に出ていて数えきれないので、1[Wb]分の磁力線のまとまりを「磁束」と呼んでいます。

磁界の強さを可視化したのが上図ですが、磁束の密度の濃いところは磁界が強く、密度が薄いところは磁界が弱いことになります。

1[m²]あたりの磁束のことを「磁束密度」と呼び、単位は[Wb/m²]になりますが、これは[T(テスラ)]という1文字でも表せます。