インピーダンスとは、抵抗のことであり、リアクタンスのことであり、抵抗とリアクタンスを合成したもののことでもあります。記号ではZで表されることが多く、単位は[Ω]です。
前項までで、交流回路の素子には抵抗、コイル、コンデンサの3つがあると紹介しました。コイルの性能はインダクタンスL[H]で、コンデンサの性能は静電容量C[F]で表すことができますが、これらの単位は抵抗R[Ω]とは違うので、変換式を使ってリアクタンスXLまたはXC[Ω]に直す必要があります。
以上のことにぴんとこない場合は、抵抗、インダクタンス、静電容量の概要のページを読み返してください。
変換式を使って抵抗もコイルもコンデンサも同じ単位[Ω]で表すことができたら、そこで初めて合成のための計算をすることができます。ただし、合成したものは抵抗ともリアクタンスとも呼びがたいので、これをインピーダンスZ[Ω]と呼んでいます。
つまり、インピーダンスとは、単位が[Ω]となるものの総称だと思ってください。また、前項にてコイルやコンデンサのリアクタンスは位相(=向き、ベクトル)を持つと説明しました。ということは、インピーダンスもベクトルで表すことができます。
インピーダンスZ[Ω]の式の一例として、以下のRLC直列回路では、インピーダンスは次のように書くことができます(RLC直列回路とは、抵抗、コイル、コンデンサが直列に並んだ回路です)。
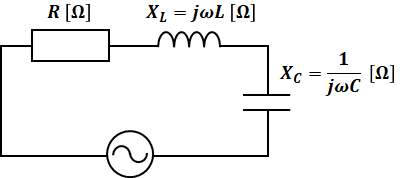
![]()
Zの上に「・」が付いているのは、これがベクトルだということを示しています。また、ωLやωCの前に「j」が付いているのは、これが複素数だということを示しています。前項での説明の通り、リアクタンスは抵抗に対して90°の位相差があるので、有効電力として使われる抵抗Rは実数部、無効電力に対応しているリアクタンスXは虚数部として表現されることが多いです。
また、上式は以下のように変換することができます(これは上式を計算しているだけなので、覚えなくても大丈夫です)。

もし問われているのが向きを含めたインピーダンスではなく、インピーダンスの大きさだったとしたら、前項で説明したのと同様、次のような三平方の定理を使うことによって計算することができます。
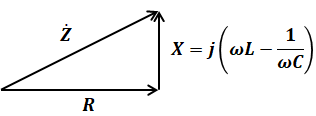
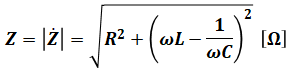
インピーダンスZは基本的にはベクトルで表されるけれど、必要に応じてその大きさを計算できるということを、その計算方法と併せて、ぜひ押さえておいてください。

コメント