三相回路の1相あたりの等価回路

三相交流回路はその回路図が単相回路に比べて複雑であるため、そのままでは電流や電圧などの計算が難しいです。そこで、三相交流は単相交流が3つ合わさったものだと考えて、1相分の回路(単相交流回路)として計算をするのが定石です。

たとえば三相交流回路における全負荷の消費電力を求めたいなら、1相分の等価回路において負荷が消費する電力を求め、あとは3相分なので「×3」をする…といった具合です。

三相交流回路は単相交流回路が3つ合わさったもの、ということを視覚的に理解するため、以下を見てください。

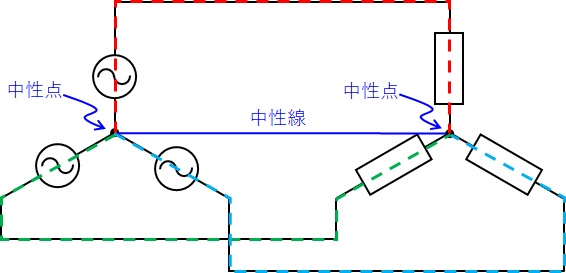
上図に記入してある通り、Y結線における中心点のことを中性点といい、2つの中性点を結んだ架空の電線のことを中性線といいます。この中性線と赤線で囲われるのが1相分の回路で、中性線と緑色線も1相分、中性線と水色線も1相分で、合計3相分となります。

よって、上記回路から1相分の等価回路を取り出すと、次のような単相回路を描くことができます。

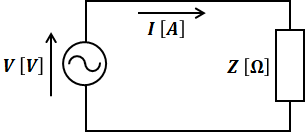
このように1相あたりの等価回路がわかれば、オームの法則を使うなどして、電圧や電流、インピーダンス、電力などを計算によって求めることができます。

ちなみに、Δ結線には中性点がないので、このように中性線を引いて1相あたりの等価回路として表現することができません。そこで、Δ結線の場合には前項で解説したΔ-Y変換を使い、Y結線のかたちに直した上で1相分の等価回路を作ることになります。

次項では、この等価回路を使った計算問題の例題を紹介します。