真空中に電子があり、もしそこに電界または磁界が存在するなら、この電子に力が働いて、電子は運動します。より具体的には、電界中では電子は等加速度運動をし、磁界中では電子は円運動をします。
前項では電界中における電子の運動を解説したので、この項では磁界中における電子の運動を解説します。
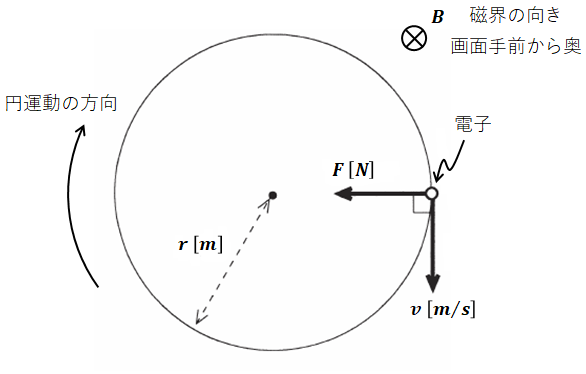
真空中において、磁束密度B[T]の一様な磁界が画面の手前から奥へ垂直に加わっているとします。このとき、以下の図のように電荷-e[C]、質量m0[kg]の電子を置き、矢印で示す向きに速さv[m/s]の初速度を与えると、この電子は、初速度の向きとも磁界の向きとも垂直になる方向の電磁力F[N]を受けます。
磁界の中を運動する電子が受けるこの電磁力F[N]のことを、ローレンツ力といい、以下の式で表されます。
![]()
- F:ローレンツ力[N]
- B:磁束密度[T]
- e:電子の電荷[C]
- v:電子の速度[m/s]
また、上記のB、e、vのそれぞれの向きは、フレミングの左手の法則に従います。これは、左手の親指と人差し指と中指を互いに直交させたとき、指の向きと電流、磁界、電磁力とが以下のように対応するという法則です。
- 中指:電流の向き(電子の速度の反対向き)
- 人差し指:磁界の向き
- 親指:電磁力の向き
今回の場合は、「電流の向き」というのが「電子の向きの反対方向」となる点に注意してください。電流は正電荷が移動する向きに進みますが、電子は負電荷が移動する方向なので、これらは真逆の向きになります。
また、電磁力はここではローレンツ力のことだと考えてください。すると、上図においては、中指を電子の速度とは反対向き(画面上向き)に合わせ、人差し指を磁界の向き(画面奥向き)に合わせると、ローレンツ力は画面左方向を向くことがわかります。
以上から、電子は進行方向とは垂直の向きにローレンツ力を受けるので、この電子は加速も減速もせず、ただ向きだけが変わります。するとカーブするように動きますが、曲がりながらもその都度その進行方向に対して垂直向きに力を受け続けるので、結果として、この電子は速度v[m/s]のまま等速円運動をすることになります。
また、この円の半径をr[m]とすると、電子の運動は、ローレンツ力と遠心力とがつり合った状態を保つので(つり合った状態とは、2つの力の大きさが同じで、向きが正反対である状態です)、左辺にローレンツ力を、右辺に遠心力を置いてイコールで結べば、以下の式のように書くことができます。
![]()
上式をrについて解けば、この円運動の半径を求めることもできます。
![]()
また、上記のパラメータを使えば、円運動の周期T[s]や各周波数ω[rad/s]を計算できます。
Tを求めるためには、まず以下の基本的な(かつ重要な)3つの式を押さえておく必要があります。
![]()
- T:周期[s]
- f:周波数[Hz]
![]()
- ω:角周波数[rad/s]
![]()
- v:速度[m/s]
- r:半径[m]
以上の3式と、先ほどのrの式から、周期Tは次のように計算できます。
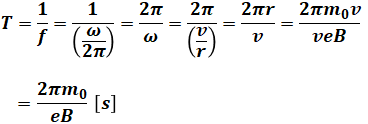
また、各周波数ωは以下の式で表すことができます。
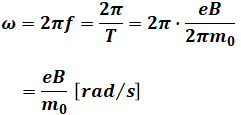
上記の2式(周期Tや各周波数ωをe、m0、Bで表す式)は暗記しておくほど頻出ではありませんので、基本式だけ押さえておいて、必要に応じてその都度計算で導出できれば充分だと思います。
一方、ローレンツ力の式や遠心力の式はぜひ覚えておきたいところです。

コメント