磁界中に導体があり、そこに電流が流れているとき、導体は磁界から電磁力という力を受けます。たとえば、磁界中に固定されていない導体を置き、そこに電流を流すと、導線が電磁力を受けてころころと転がるイメージです。ここで登場する3つのパラメータ、電流I・磁界B・電磁力Fの向きは、前項で解説した通り、フレミングの左手の法則に従います。
前項の繰り返しになりますが、フレミングの左手の法則とは、左手の親指と人差し指と中指を互いに直交させたとき、指の向きと電流I、磁界B、電磁力Fとが以下のように対応するという法則です。
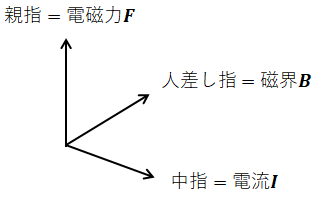
- 中指:電流Iの向き
- 人差し指:磁界Bの向き
- 親指:電磁力Fの向き
この法則を使えば向きはわかるとして、計算問題などでは電磁力F[N]の大きさも重要です。電磁力の計算式は、電流が流れている導体や磁界の配置によって変わってくるので、以下にまとめます。
磁界の向きと電流の向きが直角の場合
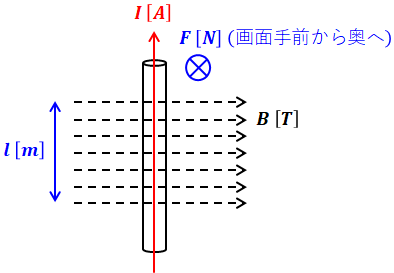
下図のように、磁束密度B[T]の磁界中をその向きに対して直角に電流I[A]が流れているとします。導体の長さ(正確には、磁界の中に置かれている長さ)をl[m](電流のアイではなく、長さのエル)とすると、電磁力の大きさは次のように表すことができます。
![]()
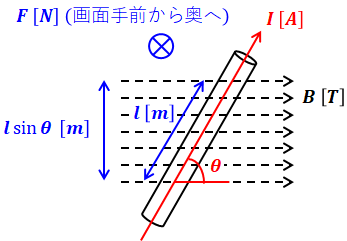
磁界の向きと電流の向きが斜めの場合
電磁力はあくまでも磁界の向きと電流の向きが直角となった際に生じる力です。そのため、もし磁界の向きと電流の向きが斜めになっているのなら、そのうち垂直成分の長さの分だけ電磁力が生じます。つまり、この場合は下図と下式のように表すことができます。
![]()
導体が平行に並んでいる場合
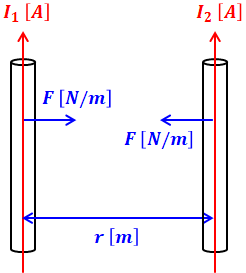
下図のように2本の導体が平行に並んでいる場合、その電流の向きが同じであれば両者の間に引力が、電流の向きが反対であれば両者の間に斥力(反発力)が電磁力として働きます。導体1[m]あたりの電磁力の大きさは、次の式によって表すことができます。
![]()
- F:導体1mあたりの電磁力[N/m]
- μ0:透磁率(真空中または空気中) 4π×10-7[H/m]
- I1、I2:電流[A]
- r:導線間の距離[m]
上式は公式として押さえておきたいところですが、その導出過程も重要なので、以下に解説します。
まず注意点として、電磁力は物理的な力なのでその単位は普通は[N]ですが、平行な導体では長さがはっきりしないので、この場合は1[m]あたりと限定して計算するのが一般的です。よって、今回のような場合には、電磁力の式は以下のように1[m]あたりで考えて、その単位も[N/m]とします。
![]()
ここで、磁束密度B[T]は、(真空または空気中の)透磁率μ0[H/m]と磁界の強さH[A/m]の積で表すことができます。
![]()
一方、直線導体による磁界の強さHは、直線導体・円形コイルによる磁界のページで紹介した通り、以下の等式が成り立ちます。
![]()
よって、以上の3式を合わせると、公式として示した式を導くことができます。
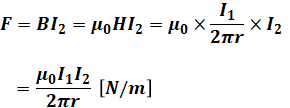

コメント