前項までで扱ってきた各種の式を使って、この項では力率の計算について例題を紹介します。
例題
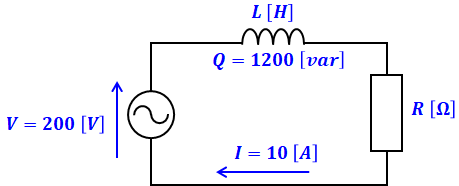
下図のように、正弦波交流電圧V=200[V]の電源が、インダクタンスL[H]のコイルとR[Ω]の抵抗との直列回路に電力を供給しています。また、この回路の定格周波数fは60[Hz]です。
この条件下で、回路を流れる電流I=10[A]、回路の無効電力Q=1200[var]とすると、抵抗R[Ω]の値と力率cosθの値、コイルのインダクタンスL[H]はいくつになるか、計算によって求めてみてください。
解説
まず、問題文に電流と電圧がすでに与えられているため、この回路の皮相電力Sは次のように計算できます。
![]()
続いて、皮相電力S[V・A]は有効電力P[W]と無効電力Q[var]の合力なので、三平方の定理を用いて計算すれば、Pを算出することができます。

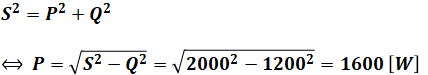
そして、有効電力Pは、抵抗を流れる電流Iと抵抗R[Ω]から求めることができるので、逆算すればRが計算できます。
![]()
これで抵抗Rの値がわかったので、続いて力率cosθを求めます。
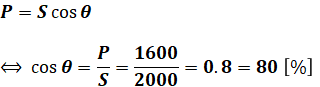
最後に、コイルのインダクタンスL[H]を求めます。コイルのリアクタンスXL[Ω]はオームの法則より、
![]()
と求められるので、インダクタンスL[H]は次のように計算することができます。
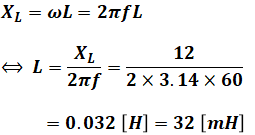
この問題ではインダクタンスの単位が[H]ですが、[mH](ミリヘンリー)で問われることもあるので、参考までに載せておきました。
また、蛇足ですが、この回路のインピーダンスZの式と、インピーダンスZの大きさは次のように計算することができます。

![]()
![]()
最後に、力率はこの問題で求めたように「皮相電力Sに対する有効電力P」という比で求めることができますが、上図からもわかるように「インピーダンスZに対する抵抗R」で求めることもできます(抵抗と有効電力の関係、インピーダンスと皮相電力の関係が同等なので、当然ともいえますが…)。
![]()

コメント