交流回路の素子には抵抗、コイル、コンデンサの3つがあります。前項までは、回路図においてこれらを別々に記載していましたが、場合によっては「負荷」としてまとめて書くことがあります。
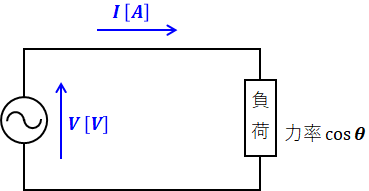
上図のような場合、負荷の記号は抵抗と同じく長方形となっていますが、これには抵抗分のほかにリアクタンス分も含んでいます。つまり、上図は敢えて描き換えるなら、たとえば以下のような回路ということになります。
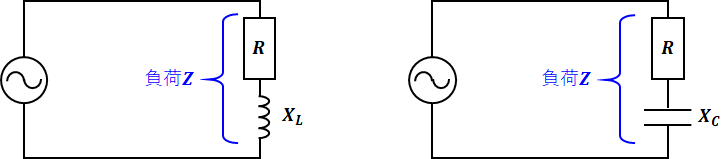
以上を前フリとして、上記を踏まえた上で、この項では交流回路の電力について解説をします。まず、直流回路においては電力Pの式は電圧Vと電流Iを使って以下のように表すことができます。
![]()
しかし、交流回路では、全ての電力のうち、抵抗で消費される電力のことを有効電力P[W]といい、コイルやコンデンサにおける電力のことを無効電力Q[var]といいます。
有効電力は、電気エネルギーがほかのエネルギー(運動エネルギーや熱エネルギー)に変換されて回路の外へ出ていきますが、無効電力はこのように消費される電力ではなく、エネルギーが負荷に蓄えられたり負荷から放出されたりすることで、負荷側と電源側を行ったり来たりします。出力として取り出せない電力なので、無効電力と呼ばれています。
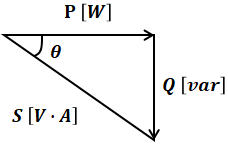
また、有効電力Pと無効電力Qを合わせた全ての電力のことを、皮相電力S[V・A]といいます。合わせた…といっても、単純な和ではありません。インピーダンスのページで説明した通り、抵抗とリアクタンスとは90°分の位相差があるので、有効電力と無効電力との間にも同じく90°の位相差があります。
よって、皮相電力S、有効電力P、無効電力Qは、以下のベクトル図のような関係となります。
ちなみに、3つの電力の単位はそれぞれ異なりますが、どれも次元は同じです(覚えなくて構いませんが、どれもSI単位系に直すと[m2・kg・s-3]になります)。また、皮相電力の単位は「ボルトアンペア」、無効電力の単位は「バール」と読みます。
以上のまとめとして、皮相電力、有効電力、無効電力を式で表すと以下の通りです(θは皮相電力のベクトルと有効電力のベクトルとの間の角度です)。ここは重要事項なので、ぜひ押さえておいてください。
![]()
![]()
![]()
![]()
上式のうち、「cosθ」のことを力率と呼んでいます(そのままcosθとして0~1で表される場合と、100倍して0%~100%で表される場合があります)。
これは、皮相電力のうち有効電力(出力)として取り出せる割合がどれくらいかを表す指標となるため、こう呼ばれています。たとえば皮相電力が100[V・A]で、そのうち有効電力が60[W]であれば、その力率cosθは0.6(60%)となります。
また、これをどうにかして有効電力80[W]に上げると力率は0.8(80%)となりますが、このようなことを力率改善といいます。

コメント