変圧器の等価回路

変圧器の概要は前項で説明した通り、その構成は以下の図のようになっています。

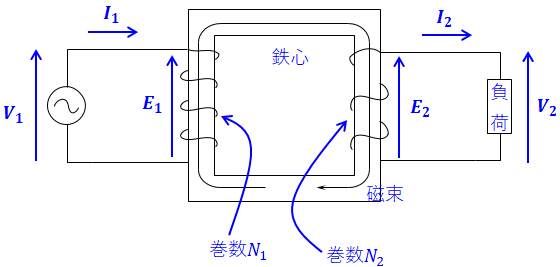
これを電気回路に直すと、次のような回路が書けます。

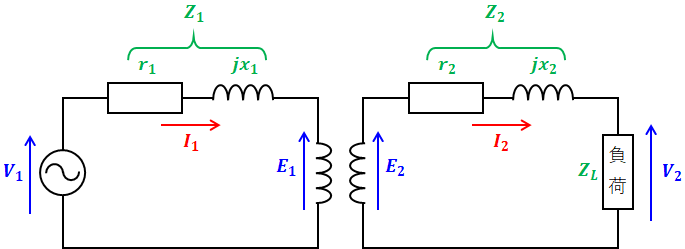
• V₁、V₂：一次電圧、二次電圧[V]
• E₁、E₂：一次側、二次側の誘導起電力[V]
• I₁、I₂：一次電流、二次電流[A]
• r₁、r₂：一次巻線、二次巻線の抵抗[Ω]
• x₁、x₂：一次巻線、二次巻線の漏れリアクタンス[Ω]
• Z₁、Z₂：一次巻線、二次巻線のインピーダンス[Ω]
• Z_L：負荷インピーダンス[Ω]

しかし、上図の電気回路は一次側と二次側の回路がそれぞれ分かれてしまっているので、変圧器の電気的な特性を考えるのが難しくなっています。そこで、電源と負荷を一緒にした1つの等価回路に置き換えると都合が良く、変圧器ではこの手法が広く用いられます。

2つの回路を1つの等価回路にするには、以下の2つの方法があります。

• 二次側の諸量を一次側に換算した等価回路
• 一次側の諸量を二次側に換算した等価回路

どちらの方法も似たようなものですが、特に上の「二次側の諸量を一次側に換算した等価回路」がよく使われています。

二次側の諸量を一次側に換算した等価回路

二次側の諸量を一次側に換算した結果、上記の電気回路は以下のように書き換えられます。

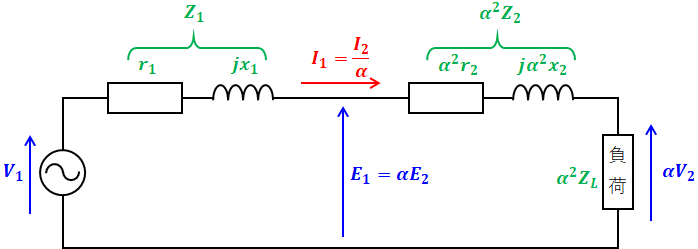
• α：巻数比(N₁/N₂)

前項にて

が成り立つと説明しましたが、これを書き換えると以下の関係式になるため、上図の等価回路が成立します。

一次側の諸量を二次側に換算した等価回路

今度は先ほどと反対に、一次側の諸量を二次側に換算すると、冒頭の電気回路は以下のように書き換えられます。

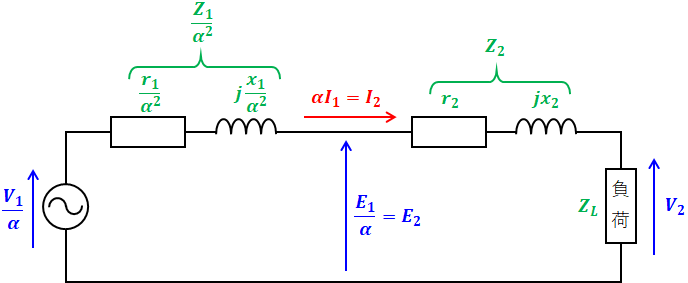
これも考え方は二次側の諸量を一次側に換算したときと同じですが、しいていえば、巻数比αの式の使い方が先ほどとは反対になります。つまり、巻数比の式を以下のような関係式として扱っています。