前項では伝達関数に関する基本的なことを解説したので、この項では、複雑なブロック線図をどのようにして簡単なブロック線図に書き直し、伝達関数として表現するか、2つの具体例を用いて説明していきます。
例1
まず1つ目の例として、以下のブロック線図を見てください。
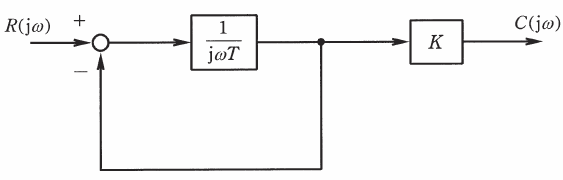
このブロック線図をブロック線図の等価交換のページで解説した等価交換を用いて、より簡単なブロック線図に変換します。これはフィードバック結合と直列結合を連続して持ちいることで1つのブロックにまとめることができます。
フィードバック結合の公式は、
ですが、今回は
で、G2の位置にはブロックが何もないので、
となります。また、分母の±の符号は負のフィードバックなら+、正のフィードバックなら-です。よって、フィードバック結合によってできる式は、
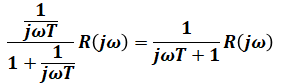
となり、さらに右側のブロック(K)との直列結合になるため、このブロック線図の最終的な伝達関数は、
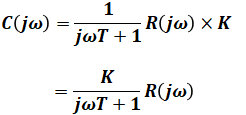
となります。
例2
続いて、以下のブロック線図の伝達関数がどうなるかを考えていきます。
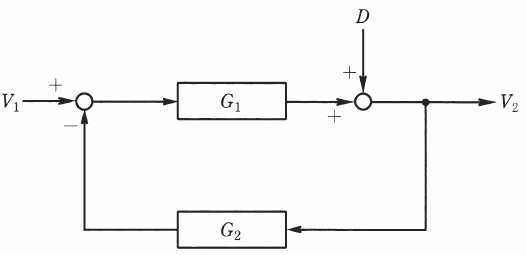
この場合も先ほどの例題と同様のフィードバックの形があるので、フィードバック結合の公式を使いたいです。しかし、現状のままではDの入力が邪魔な位置にあるので、まず初めに、これを移動させることを考えます。
ブロック線図の等価交換のページで紹介した「加え合わせ点の手前への移動」を使うと、上図は下図のように描き換えることができます。
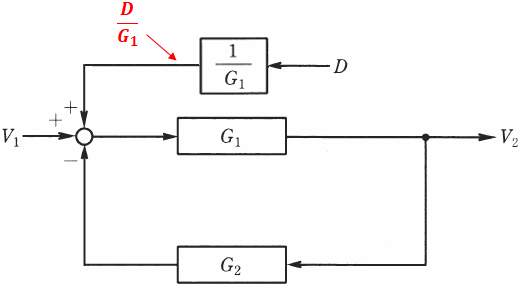
上図を見てもわかる通り、赤字で示した箇所は、Dと1/G1との直列結合のため、積で表すことができます。すると、フィードバック結合の公式である
のうち、入力がV1と
の和なので
となり、G1とG2は公式の通りそのまま使えます。また、分母の±の符号は負のフィードバックなら+、正のフィードバックなら-です。そして、出力はV2なので、このブロック線図の伝達関数は、
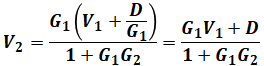
と表すことができます。
例2の別解
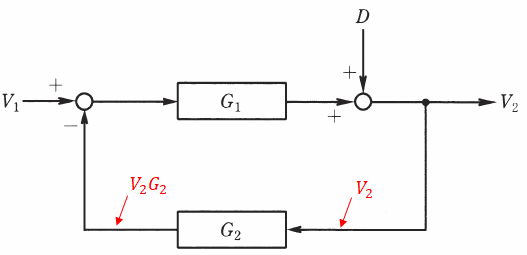
また、この問題を「加え合わせ点の手前への移動」を直接用いずに、以下のように1箇所ずつ考えて解くこともできます。
最初はG2のブロックに向かって伸びている矢印のところを考えます。これは図の一番右側にあるV2と同じ引き出し点(●)から出ているので、ここもV2になります。またG2のブロックの直後はV2とG2の直列結合なので、V2G2となります。
続いて、G1のブロックの手前はV1と先ほど算出したV2G2との並列結合なので、V1-V2G2となります。その後は、これとG1との直列結合になるので、(V1-V2G2)G1となります。
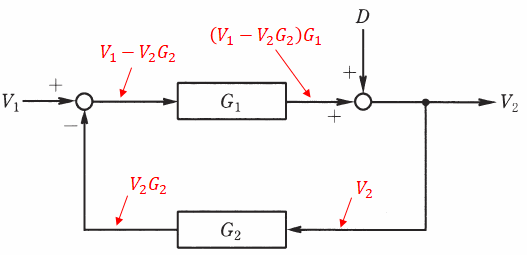
また、これとDとが加え合わせ点(○)により並列につながっているため、V2は、
となります。
あとはこの式をV2について解くと
となって伝達関数ができあがります。
このように、重要なブロック線図の等価交換ルールを覚えておけば、伝達関数はそれらを組み合わせることで導き出すことができます。
コメント