伝達関数とは、制御系における入力と出力の関係を示す式のことです。
伝達関数というものを本当に理解するためには、ラプラス変換の知識が欠かせません。伝達関数においては制御系の入出力の式を複素数領域(s領域)で表すことが多いのですが、これは、比較的簡単に表現できる時間領域(t領域)をラプラス変換することによって求められます。
具体的には、伝達関数を要素によって分類し、一次遅れ要素、二次遅れ要素、積分要素、微分要素といった分類ごとに複素数領域(s領域)の式を学んでいくと、伝達関数を体系的に理解できるようになります。
…が、こと電験三種の試験に限定して話をすると、上記でいう複雑な式を習得しても、あまり点数につながらないかもしれません。
伝達関数というのは要するに、前項までで解説してきたブロック線図を式にしたもののことなので、前項までに扱ってきた頻出のブロック線図について、それらを式に変換できればそれで充分ということになります。
よって、この項では、ブロック線図の等価交換のページで紹介したブロック線図について、代表的な伝達関数を紹介するに留めます(より詳しい内容に興味のある方は、ぜひ別の本やサイトを調べて勉強してみてください。試験合格という目的にとらわれなければ、決して無駄にはならないと思います)。
フィードバックの伝達関数
フィードバックの伝達関数は最も重要なので、ぜひ覚えておいてほしいです。
前項にて、下図の左側のようなフィードバックモデルは右側のように簡略化できることを紹介しました。
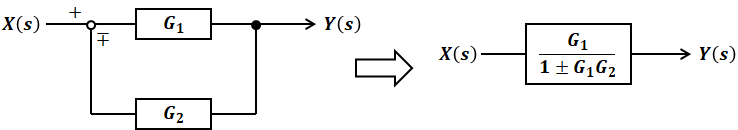
そのため、入力をX(s)、出力をY(s)とすると、
![]()
と表すことができます。図中の「∓」が、式では「±」とひっくり返ることに注意してください。
しつこいようですが、これは公式として覚えてしまうことをおすすめします。
直列、並列の伝達関数
直列または並列のときは、それぞれ、積と和(差)で結合できることを前項で紹介しました。そのため、これらの伝達関数もやはり積や和(差)で表すことができます。
つまり、入力をX(s)、出力をY(s)とすると、直列の場合は
![]()
![]()
となり、並列の場合は
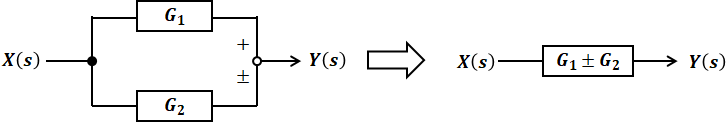
![]()
のように書くことができます。
ここではこれ以上の例は出しませんが、伝達関数というのは入力とその間の制御を用いて出力の式を表すことなので、前項で紹介したブロック線図の等価交換をうまく使い、なるべくシンプルなブロック線図を作ることが重要です。
上で紹介した例のように、ブロックをただ1つにすることができれば、伝達関数は「Y(s)=(ブロック内の式)×X(s)」と書くことができます。
理屈としては上記のことだけ押さえておけばひとまず充分だと思いますが、具体例がないと考え方が定着しづらいかもしれないので、次項では、より実践的なブロック線図を使って、そこから伝達関数を作り上げることについて考えていきます。

コメント