前項では単相半波整流回路について解説したので、この項では単相全波整流回路について紹介します。前項の内容がある程度わかっていることを前提としていますので、未読の方は先に整流装置(単相半波整流回路)のページをご確認ください。
単相全波整流回路
単相半波整流回路のときは、抵抗の電圧が正の向きのときだけ出力として現れてきましたが、単相全波整流回路では抵抗の電圧の向きにかかわらず、出力されます。そのためには、サイリスタを用いて以下のような回路図を組みます。
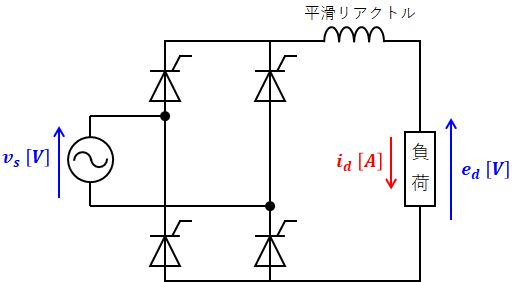
単相半波整流回路のページで解説したのと同様、単相全波整流回路においても、負荷側がただの抵抗負荷である場合と平滑リアクトルを設けて回路全体の負荷が誘導性負荷となっている場合の2パターンがあります。
負荷が抵抗負荷か誘導性負荷かによって出力電圧edと電流idの波形が異なった軌跡となるので、以下ではこれら2パターンをそれぞれ紹介していきます。
まずは負荷が抵抗負荷(力率1)である場合について考えます。この場合、上記で示した回路図のうち、平滑リアクトルはないものとして考えてください。
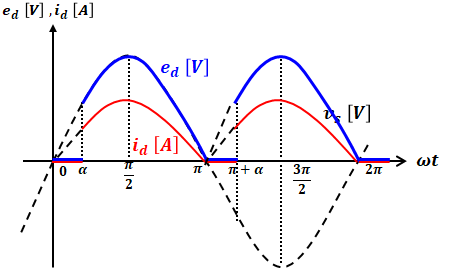
抵抗負荷の場合には、電源電圧vsと出力電圧ed、電流idの関係は以下の図のようになります。要するに、基本は単相半波整流回路の形と同様である一方、電源電圧vsが負であっても電圧edと電流idは正になるという話です。
【抵抗負荷の場合】
単相全波整流回路も単相半波整流回路のときと同様、出力の直流平均電圧Edを計算することができます。その式は、以下の通りですが、要するに単相半波整流回路と比べると半波だったのが全波に変わるだけなので、単純に単相半波整流回路のときの2倍になると覚えておけば大丈夫です。
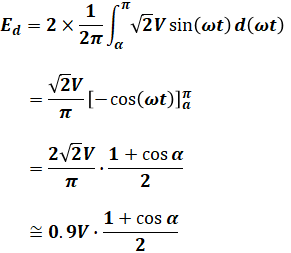
ちなみに、上式はサイリスタを使った式ですが、もしダイオードを使った問題が出題された場合は、上式にα=0を入れればよいです。つまり、Ed=0.9V [V]となります。
続いて、平滑リアクトルを設けて回路全体の負荷が誘導性負荷(RとLの組合せ)になっている場合について考えます。これも単相半波整流回路のときの挙動をしっかり押さえておけば、半波が全波に変わるだけなので話はわかりやすいです。
電源電圧vs、出力電圧ed、電流idの波形と、直流平均電圧Edの式は以下のように表すことができます。
【誘導性負荷の場合】
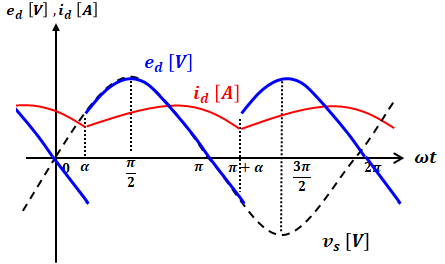
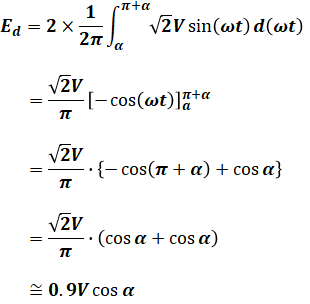
最初に示した回路図と見比べると、α≦θ<π+αの区間は左上と右下のサイリスタに電流が流れ、π+α≦θ<2π+αの区間は左下と右上のサイリスタに電流が流れる…といった具合です。
また、ここでは電流のグラフをなだらかなカーブとして描いていますが、条件さえ揃えばほぼ一直線の安定した値にすることも可能です。

コメント