交流を直流に変換することを整流(順変換)といい、この装置を整流装置、これを使った回路を整流回路といいます。整流装置に使われるパワー半導体デバイスは、整流ダイオードやサイリスタです。
整流回路には、単相であるか三相であるか、電圧の出力の範囲(半波か全波か)によってさらに種類分けされます。この項では、単相半波整流回路について扱い、単相全波整流回路は次のページで、三相整流回路はそのまた次のページで紹介します。
単相半波整流回路
以下の回路は、サイリスタを使った最も単純な単相半波整流回路の例です。
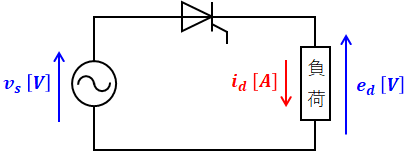
このような回路により、上図左側の交流電源を元にして右側の負荷で直流電圧として出力するのが、整流の基本です。
この回路において、まずは負荷が抵抗負荷(力率1)である場合を考えます。
サイリスタにゲート電流を流すと、電源電圧vsと出力電圧ed、電流idの関係は、以下の図のようになります。
【抵抗負荷の場合】
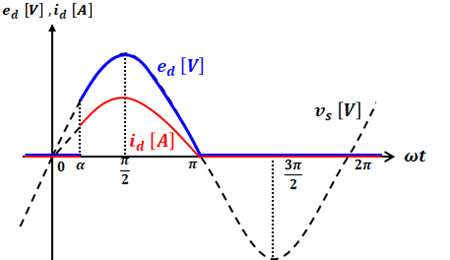
上図について、まず最初の状態(ωt=0)ではサイリスタはオフしています。これがωt=α(αはサイリスタの制御遅れ角)に達すると、ターンオンして電流が流れ始め、負荷に電圧が掛かってきます。その後、ωt=πになると電源電圧vsが負になるのでサイリスタに逆電圧が掛かってターンオフするため、回路には再び電流が流れなくなります。
このような周期により、α≦ωt≦πの間だけ、負荷には直流電圧が掛かることになります。
また、上図の波形はその瞬間ごとの出力電圧(変換後の直流電圧)を表していますが、実際に大事になってくるのは一瞬の電圧ではなく、全体で考えた際の平均電圧です。直流平均電圧(出力電圧edの平均値)をEdとすると、Edは次式で表すことができます(Vは電源電圧vsの実効値)。
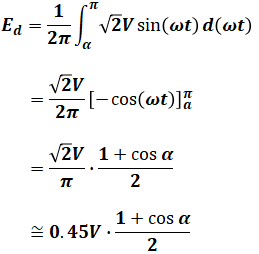
上式は、重要公式としてぜひ押さえておきたい式のひとつです。
ちなみに、この項では整流装置に使われるパワー半導体デバイスがサイリスタであることを前提に説明しましたが、試験問題によってはダイオードとして出題されるかもしれません。
もしダイオードが出題された場合には、上記のうち、α=0として考えてください。つまり、Ed=0.45V [V]となります。
より複雑なサイリスタの場合さえ押さえておけば、ダイオードの出題に対応することが可能なので、試験対策としてはサイリスタの式を公式として押さえておくことをお勧めします。
上記は負荷が抵抗負荷(力率1)である場合でしたが、これに対し、以下の回路図のように出力側にリアクトルを設けることがあります。
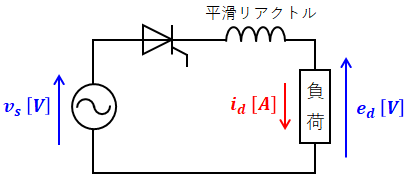
リアクトルを設けることで負荷を流れる電流の振れ幅が小さくなり、電流が平滑化されて安定した直流が得られるというメリットがあります。このように、負荷を流れる電流を平滑化する目的で置かれているリアクトルのことを、平滑リアクトルと呼びます。
平滑リアクトルがある場合、回路全体の負荷が誘導性になっているので、インダクタンスの影響で電流の立ち上がりが電圧に対して遅れ、また、ωt=πでサイリスタがターンオフしたあとも少しの間(消弧角βの分だけ)電流が流れ続けます。
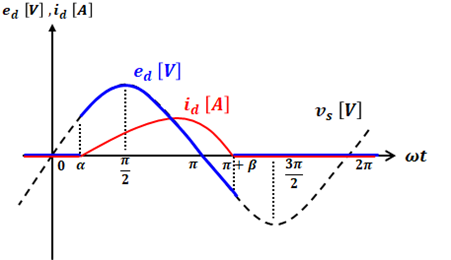
よって、電源電圧vsと出力電圧ed、電流idの関係は、以下の図のようになります。
【誘導性負荷の場合】

コメント