照度については照明の記号と単位(その他)で解説したとおり、以下の式で表されます。
![]()
- E:照度[lx]
- F:光束[lm]
- A:面の面積[m2]
これを覚えておけば基本的には大丈夫なのですが、多くの場合、面積Aが問題文で直接与えられません。よって、どうやって面積Aを求めるかが照度計算のポイントになります。
斜めからの入射
太陽は一年じゅう不変であるのに、夏の陽射しはきつくて、冬の陽射しは穏やかです。その理由は季節によって太陽光の入射角が変わるため(=太陽の高度が変わるため)です。
太陽に限らずどの光源であっても、真上(垂直)から照らせば照度は大きくなり、斜めから照らせば照度は小さくなります。
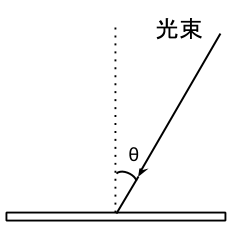
これを式にすると、以下のようになります。
![]()
- E:照度
- E’:垂直に入射したときの照度
- θ:入射角
球面の照度
ある点光源があるとき、そこから一定の距離だけ離れた地点(球面上の点)はどこも同じ照度となります(線光源のような場合はまた話が違ってきます。点光源のように一点から放射状に照射される場合の話です)。
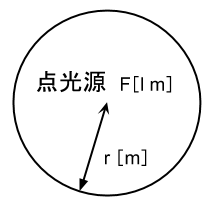
この場合、球面上のある点の照度が知りたければ最初に紹介した公式E=F/A[lx]を用いればいいのですが、ここで面積Aに注目します。球の面積は4πr2なので、球面の照度は以下のようになります。
![]()
複数の光源
ある地点の照度を求める際、光源が複数ある場合があります。しかし計算方法は簡単で、各々の光源からの照度を計算して、それらを足し算すればいいだけです。
複数の光が重なったとき、それらは相乗効果で輝くわけでも干渉しあって暗くなるわけでもありません。普通に足せばよい(=相加効果)だけなので、これさえ知っておけばこの手の問題はサービス問題といえます。

コメント