論理回路の入力と出力

前項では論理回路に用いられる記号とその意味について紹介したので、この項では論理回路全体を考えたときの入力と出力の関係について解説します。

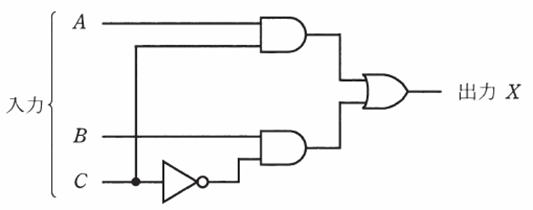
上図の論理回路は入力がA、B、Cの3つあり、それぞれに0または1を入力することができるため、入力の組み合わせは全部で8通りあります。今回は、そのうち、(A,B,C)=(0，0，0)、(1，1，1)、(1，1，0)の3通りについて具体的に考えてみます。

(A,B,C)=(0，0，0)

入力を全て0としたとき、論理回路における各値は以下のようになります。

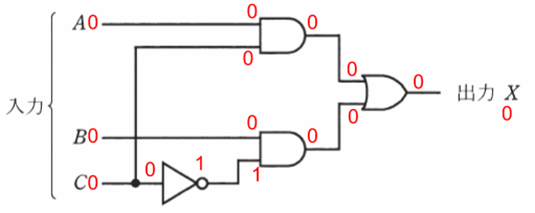
前項の復習ですが、「NOT」は強制的に入力と出力の数字が変わりますので、今回は0で入っているため、1で出てきます。「AND」は2つの入力がともに1でないと出力が1になりませんので、今回は2つとも出力が0になります。「OR」は2つの入力のうち片方でも1であれば出力も1になりますが、今回は2つとも0なので、出力も0になります。

以上より、入力が(A,B,C)=(0，0，0)のとき、最終的な出力は、X=0となります。

(A,B,C)=(1，1，1)

入力を全て1としたとき、論理回路における各値は以下のようになります。

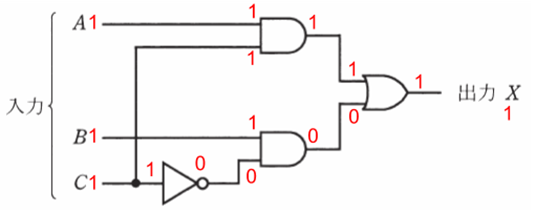
先ほどと同様に考えると、「NOT」は強制的に入力と出力の数字が変わり、今回は1で入って、0で出てきます。「AND」は2つの入力がともに1でないと出力が1になりませんので、上側の「AND」は1、下側の「AND」は0となります。「OR」は2つの入力のうち片方でも1であれば出力も1になるため、今回は出力が1になります。

以上より、入力が(A,B,C)=(1，1，1)のとき、最終的な出力は、X=1となります。

(A,B,C)=(1，1，0)

入力を(A,B,C)=(1，1，0)としたとき、論理回路における各値は以下のようになります。

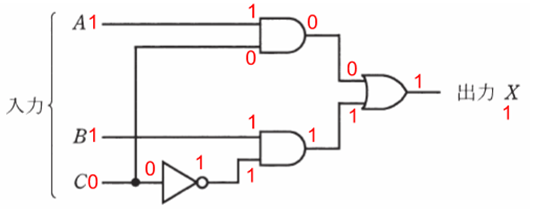
先ほどと同様に考えると、「NOT」は強制的に入力と出力の数字が変わり、今回は0で入って、1で出てきます。「AND」は2つの入力がともに1でないと出力が1になりませんので、上側の「AND」は0、下側の「AND」は1となります。「OR」は2つの入力のうち片方でも1であれば出力も1になるため、今回は出力が1になります。

以上より、入力が(A,B,C)=(1，1，0)のとき、最終的な出力は、X=1となります。

上記の通り、この例では入力の組み合わせが全部で8通りありますが、以上のように考えていけば、ほかの組み合わせについても出力がどうなるかを導き出すことができると思います。

8通り全ての結果を以下の表に示しますので、ぜひ自分でやってみた結果と合うか確認してみてください。