エレベータの昇降

以下の図は、電動機によるエレベータの昇降を図示したものです。

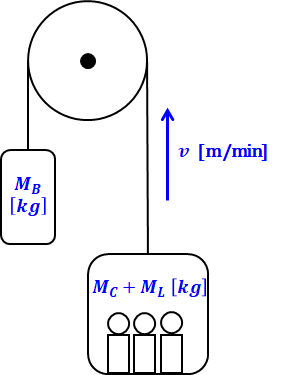
上図において、右下の四角形はエレベータのかごを示していて、かご質量はM_C[kg]です。その中にいる人(または荷物)が描かれていますが、積載質量をM_L[kg]で表しています。また、左にある四角形は釣り合いおもりと呼ばれるもので、この質量をM_B[kg]とします。

エレベータを上昇させようとする際、そのままかごを持ち上げようとするとM_C+M_L[kg]を重力に逆らって上げなければいけませんが、釣り合いおもりがある場合、M_B[kg]の重力の分だけ、かごを持ち上げる電動機の出力が小さくて済むようになっています。

最も効率良くエレベータの昇降ができるのは、M_C+M_L[kg]とM_B[kg]が等しい場合で、このとき電動機の必要トルクが最小になります。ただし、積載質量であるM_L[kg]はエレベータを使うたびに変化するので、実際には通常使用の積載質量を推測して設計します。

つまり、釣り合いおもりM_B[kg]は、

• α：係数(0.3～0.5くらいのことが多い)
• M_n：定格積載質量 [kg]

と表すことができます。

また、エレベータの昇降に使用する電動機の出力P[W]は次の式で求めることができます。この式は重要ですので、ぜひ押さえておいてください(といっても、位置エネルギーの考え方を使えば難しくはないと思います)。

• P：電動機の出力 [W]
• M：実質の質量 [kg] (M＝M_C＋M_L－M_B)
• g：重力加速度 9.8 [m/s²]
• v：昇降速度 [m/min]
• η：機械効率 [%]

昇降速度は問題文では分速として与えられることが多いですが、計算の際には秒速に直す必要があるので注意してください。また、電動機の効率は100%ではなく、どうしてもある程度の損失が出てしまうので、右辺では機械効率で割っています。