直流電動機の種類についてはこちらのページで、回転速度やトルクの計算式についてはこちらのページで紹介してきました。これらからもわかる通り、回転速度やトルクは端子電圧や各種電流などの値によって変動します。
パラメータ(変数)が多いままでは回転速度やトルクの変動について考えるのが難しいため、端子電圧と界磁電流を一定として、負荷電流の変動に対する回転速度やトルクの変動を見ることが多いです。この条件下での回転速度の変動の仕方を回転速度特性、トルクの変動の仕方をトルク特性といいます。
これらの特性は横軸に負荷電流I[A]、縦軸に回転速度n[min-1]またはトルクT[N・m]をとってグラフにするとわかりやすいので、以下に他励電動機、分巻電動機、直巻電動機、複巻電動機のそれぞれについてグラフを紹介します。
他励電動機
他励電動機の回転速度特性とトルク特性のグラフは以下の通りです。
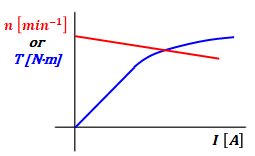
回転速度特性については、切片が正で、右肩下がりの直線となります(細かい説明は省略しますが、直流電動機の逆起電力、回転速度、トルクのページで紹介した式から直線の式を出すこともできます)。
トルク特性については、負荷電流がある程度小さい間は比例の直線になりますが、ある程度以上だと電機子反作用による影響が現れて、線が寝るような感じに推移します。
分巻電動機
分巻電動機の回転速度特性とトルク特性のグラフは以下の通りです。
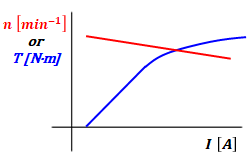
分巻電動機は、グラフを見てもわかる通り、ほとんど他励電動機と同じような軌跡を描きます。違うところを挙げるなら、全体的に(回転速度特性もトルク特性も)縦軸原点からやや右寄りになっていることです。
これは、他励電動機には界磁電流という概念がないので負荷電流I[A]=電機子電流Ia[A]となりますが、分巻電動機では負荷電流I[A]=電機子電流Ia[A]+界磁電流If[A]であるため、I[A]が0にはならないことが理由です。
直巻電動機
直巻電動機の回転速度特性とトルク特性のグラフは以下の通りです。
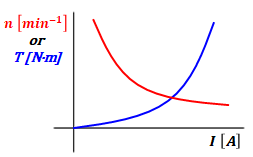
回転速度特性については、反比例の軌跡を描きます。
また、トルクは原点を通る二次関数の曲線となります。
複巻電動機
複巻電動機の回転速度特性とトルク特性のグラフは以下の通りです。
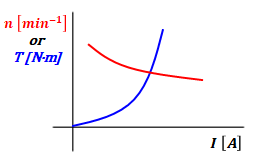
複巻電動機は分巻電動機と直巻電動機の特性を合わせた結果、上のようなグラフになります。
回転速度特性に関しては右肩下がりの直線と反比例の間と取るように、緩やかな曲線を描きます。
トルクに関しては右肩上がりの直線と二次関数の曲線の間と取るように、ややシャープな曲線を描きます。
ちなみに、このグラフは複巻電動機の中でも、和動複巻というタイプの特性のグラフです。このほか、差動複巻というタイプもありますが、あまり主流ではない上、電験三種でも過去10年以上に渡って差動複巻については触れられていないので、ここでは差動複巻については割愛します。
コメント