問 題
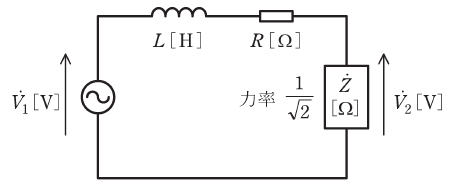
図のように、角周波数のω[rad/s]の交流電源と力率
の誘導性負荷
との間に、抵抗値R[Ω]の抵抗器とインダクタンスL[H]のコイルが接続されている。
R=ωLとするとき、電源電圧
と負荷の端子電圧
との位相差の値[°]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
- 0
- 30
- 45
- 60
- 90
解 説
抵抗Rの位相は0°であり、コイルのリアクタンスの位相は90°の遅れとなります。また、誘導性負荷のインピーダンスは抵抗分とリアクタンス分の合力なので、位相がどのくらいの進み・遅れになるかは力率によって異なります。
この問題ではととの位相差が問われていますが、のほうが考えやすいので、まずはこちらの位相を考えます。
は力率の誘導性負荷の端子間電圧なので、その位相は下図のように45°の遅れとなります。これは、ここを流れる電流が電圧に対して45°遅れているという意味になります。
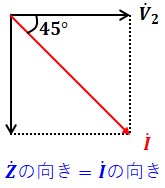
ちなみに、より、三平方の定理を使えば45°というのは簡単にわかるとして、遅れなのか進みなのかは悩むかもしれません。しかし、これは問題文に「誘導性負荷」と書いてある点からわかります。
誘導性負荷なら「抵抗とコイルが合わさったもの」、容量性負荷なら「抵抗とコンデンサが合わさったもの」と考えてください。また、誘導性負荷なら「遅れ」、容量性負荷なら「進み」となります。
続いて、について考えます。
これは電源のところなので、回路全体のインピーダンスを考える必要があります。直列回路であることから、回路全体のインピーダンスは「抵抗」と「コイルのリアクタンス」と「誘導性負荷のインピーダンス」の3つのベクトル和によって求めることができます。
とはいえ、この問題はそんなに複雑ではありません。問題文にR=ωLと書いてあるので、「抵抗」と「コイルのリアクタンス」の合力は直角二等辺三角形になるので、力率はであり、45°の遅れとなることがわかります。
ここにさらに力率の誘導性負荷を足し合わせるのですが、全く同じ方向のベクトルを足し合わせているので、合力の向きもそのままです。
以上から、電源電圧と負荷の端子電圧はどちらも位相が同じなので、その位相差は0となります。
よって、(1)が正解です。
コメント