問 題
次の文章は、帯電した導体球に関する記述である。
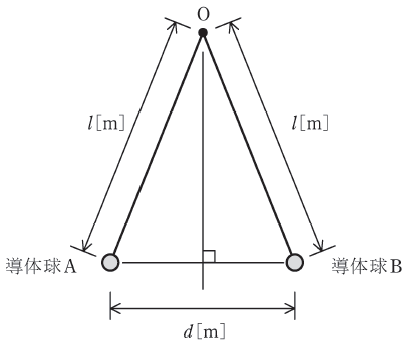
真空中で導体球A及びBが軽い絶縁体の糸で固定点Oからつり下げられている。真空の誘電率をε0[F/m]、重力加速度をg[m/s2]とする。A及びBは同じ大きさと質量m[kg]をもつ。糸の長さは各導体球の中心点が点Oから距離l[m]となる長さである。
まず、導体球A及びBにそれぞれ電荷Q[C]、3Q[C]を与えて帯電させたところ、静電力による( ア )が生じ、図のようにA及びBの中心点間がd[m]離れた状態で釣り合った。ただし、導体球の直径はdに比べて十分に小さいとする。
このとき、個々の導体球において、静電力F=( イ )[N]、重力mg[N]、糸の張力T[N]、の三つの力が釣り合っている。三平方の定理よりF2+(mg)2=T2が成り立ち、張力の方向を考えると![]() は
は![]() に等しい。これらよりTを消去し整理すると、dが満たす式として、
に等しい。これらよりTを消去し整理すると、dが満たす式として、
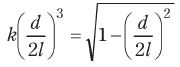
が導かれる。ただし、係数k=( ウ )である。
次に、AとBとを一旦接触させたところAB間で電荷が移動し、同電位となった。そしてAとBとが力の釣合いの位置に戻った。接触前に比べ、距離dは( エ )した。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
( ア )について、電荷は+と-なら引き合いますが、+同士や-同士だと反発力が働きます。今回は導体球A、Bともに+なので、( ア )には「反発力」を入れるのが適切です。
( イ )について、静電気力の公式は以下の通りです。これは最重要公式として必ず押さえておきたい数式です。
![]()
- F:静電気力[N]
- ε0:真空の誘電率 8.854×10-12[F/m]
- Q:電荷[C]
- d:電荷間の距離[m]
今回は上式のQ1とQ2にそれぞれQと3Qを入れればよいので、以下のように計算することができます。
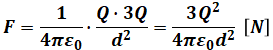
( ウ )について、問題文によると、三平方の定理の式を整理したものが係数kを含んだ式になるということです。そのため、この定理の式を起点に考えます。
![]()
ここで、問題文でF/T=d/2lと与えられている上に、kを含む等式の両辺に「d/2l」という形が残っているため、上式を変形して「F/T」の形を作った上で「d/2l」を代入します。
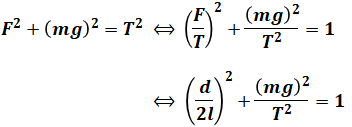
このあとの式変形には様々なやり方がありますが、選択問題である限りは選択肢に合うような形にしなければなりません。選択肢を見ると、(1)~(5)のいずれも「mg」がこの形で存在します。
上式では「(mg)2」となっているので、この相違を意識しながら以下のように式変形します(このあたりの計算は種々のやり方があります。以下は一例です)。
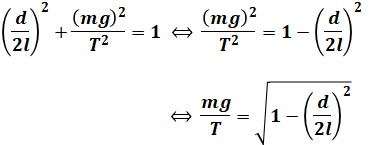
これで上式の右辺は問題文の式と一致しました。左辺については、問題文にあるF/T=d/2lという式と( イ )で求めた結果を使うと、以下のように式変形できます。
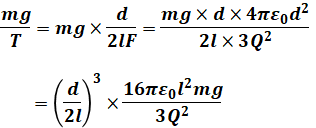
「(d/2l)3」でくくっているところは強引な式変換に思えるかもしれませんが、問題文の等式の左辺がこうなっているので、それに合わせただけです。
よって、係数kは次のようになります。これが( ウ )の答えです。
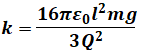
( エ )について、2つの導体球を接触させた場合、電荷が移動することはあっても総量が変わることはありません。つまり、Qと3Qだったものが同電位になったとすれば、それは2Qと2Qになっています(合計は4Qで不変です)。
接触前後の反発力Fの式は以下のように表すことができます。
- 接触前(Qと3Q)
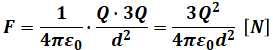
- 接触後(2Qと2Q)
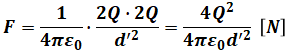
接触後の反発力Fは接触前と変わらないので、分子が大きくなったということは分母も大きくなるはずです。よって、距離dも大きくなると判断できるので、( エ )には「増加」が入ります。
以上から、
- ア:反発力
- イ:3Q2/4πε0d2
- ウ:16πε0l2mg/3Q2
- エ:増加
となるので、正解は(1)です。

コメント