電験三種 H30年 機械 問17 問題と解説

　問 題　　　　　

どの方向にも光度が等しい均等放射の点光源がある。この点光源の全光束は15000lmである。この点光源二つ(A及びB)を屋外で図のように配置した。地面から点光源までの高さはいずれも4mであり、AとBとの距離は6mである。次の(a)及び(b)の問に答えよ。

ただし、考える空間には、A及びB以外に光源はなく、地面や周囲などからの反射光の影響もないものとする。

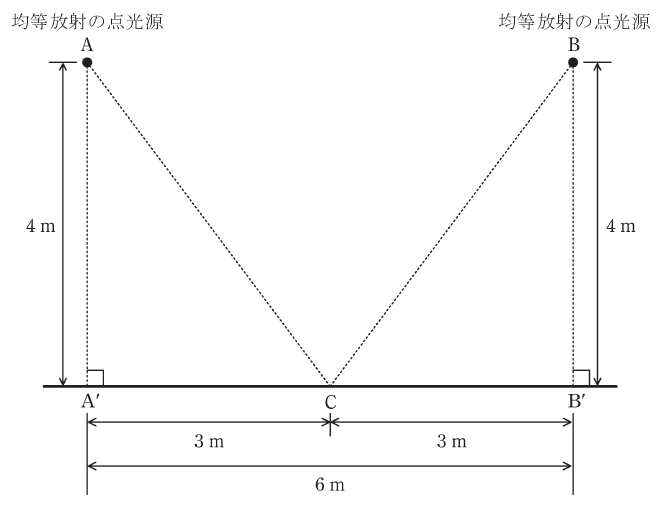
(a)　図において、点光源Aのみを点灯した。Aの直下の地面A’点における水平面照度の値[lx]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 56
2. 75
3. 100
4. 149
5. 299

(b)　図において、点光源Aを点灯させたまま、点光源Bも点灯した。このとき、地面C点における水平面照度の値[lx]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 46
2. 57
3. 76
4. 96
5. 153

 

 

 

 

 

　解 説　　　　

(a)

光束が与えられていて照度が問われているので、この2つを結ぶ以下の式を使います。

• E：照度[lx]
• F：光束[lm]
• A：面の面積[m²]

ここで、問題文に「どの方向にも光度が等しい均等放射の点光源」と書かれているので、上式のAは、半径r[m]の球体の面積ということなります。

よって、以下のように計算すれば求める答えが得られます。

以上から、正解は(2)です。

(b)

2つの光源から光を受けた場合、その照度は単純に足し合わせることができます。つまり、点Cにおいて、点光源Aによる水平面照度と点光源Bによる水平面照度をそれぞれ求めて、その和が答えとなります。

ただし、問題の図を見てもわかる通り、点Cを中心に左右対称(光源までの距離や角度が一緒)の図となっていて、さらに点光源Aと点光源Bの全光束も同じです。ということは、それぞれを計算しなくても、片方を計算して2倍すればそれが答えということになります。

よって、以下では点光源Aについてだけ考えます。

まずは「水平面照度」というのにこだわらず、点光源Aによって点Cの照度E_Cがいくつになるのかを(a)と同じように計算します。このとき、ACの距離r_Cは三平方の定理から求めます。

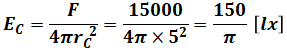
ただし、ここで求めた照度というのは水平面照度ではなく、点光源と向き合った方向の照度となります。水平面照度E’_Cについて考えるには以下の図を見てください。

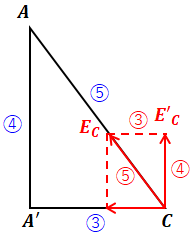
上図のように、E_CはCからAに向かっていく方向のベクトルで表すことができますが、求めたいのは水平面照度なので、E’_Cのベクトルです。

△AA’Cが3：4：5の直角三角形であることはすでにわかっているので、ベクトルE’_Cを含む三角形についても相似のため、上図赤丸の数字の比が成り立ちます。よって、E’_Cは以下のように求めることができます。

これで点光源Aによる水平面照度がわかりましたが、最初に説明したように点光源Bからの影響も全く同じなので、上式の結果を2倍したものが最終的な答えとなります。

よって、正解は(3)となります。