問 題
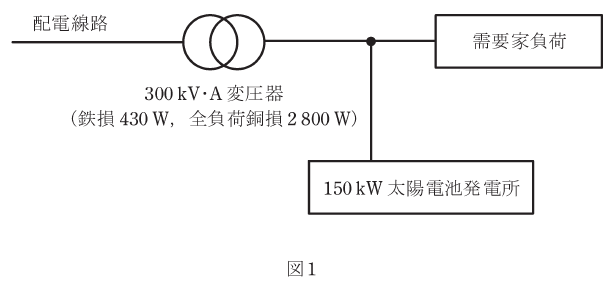
ある需要家では、図1に示すように定格容量300kV・A、定格電圧における鉄損430W及び全負荷銅損2800Wの変圧器を介して配電線路から定格電圧で受電し、需要家負荷に電力を供給している。
この需要家には出力150kWの太陽電池発電所が設置されており、図1に示す位置で連系されている。
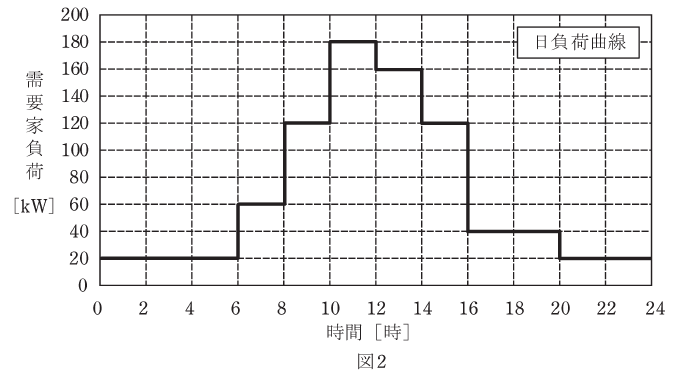
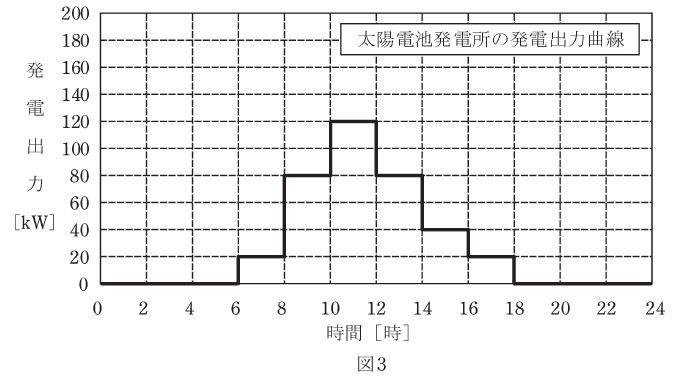
ある日の需要家負荷の日負荷曲線が図2であり、太陽電池発電所の発電出力曲線が図3であるとするとき、次の(a)及び(b)の問に答えよ。
ただし、需要家の負荷力率は100%とし、太陽電池発電所の運転力率も100%とする。なお、鉄損、銅損以外の変圧器の損失及び需要家構内の線路損失は無視するものとする。
(a) 変圧器の1日の損失電力量の値[kW・h]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 10.3
- 11.8
- 13.2
- 16.3
- 24.4
(b) 変圧器の全日効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 97.5
- 97.8
- 98.7
- 99.0
- 99.4
解 説
(a)
問われているのは損失電力量ですが、これには鉄損(無負荷損)と銅損(負荷損)の2種類があります。よって、鉄損と銅損をそれぞれ求めて、それらを足したものが答えとなります。
鉄損(無負荷損)は負荷が掛かっていても掛かっていなくても関係なく発生します。これは問題文より430[W]なので、1日あたりの鉄損P鉄は次のように計算できます。
![]()
一方、銅損(負荷損)は負荷が掛かっているときだけに発生する損失です。そのため、まずは変圧器にどのくらいの負荷が掛かっているかを調べるために、問題の図2と図3を見比べてみます。
図2は需要家負荷をグラフ化したものであり、図3は太陽光発電による電力の供給をグラフ化したものなので、その差し引きの分が、変圧器を介して供給される電力ということになります。
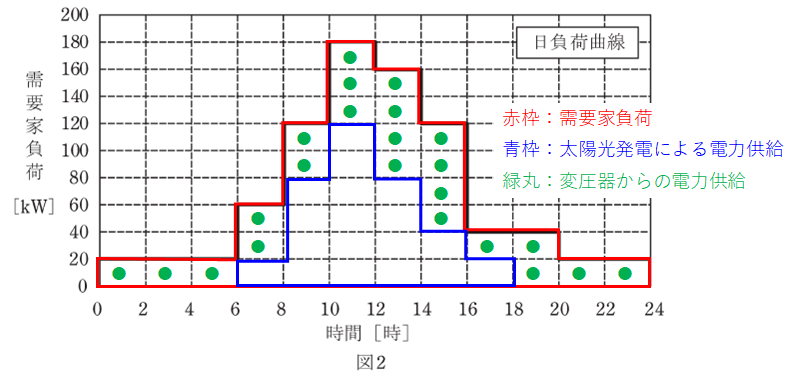
上図において、赤枠が需要家負荷、青枠が太陽光発電による電力供給を示し、その差分となる緑丸が変圧器からの電力供給を表しています。これから計算で出したいのは変圧器の銅損なので、上図から変圧器の出力分だけを取り出すと、下図のように描き換えることができます。
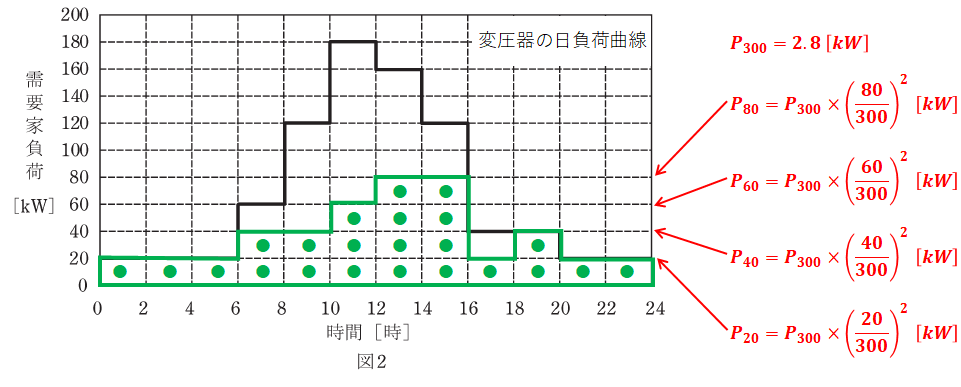
上図の右側にはすでに数式を示していますが、この意味について説明します。
銅損は負荷の掛かり方によってその値が変化しますが、それは電流の2乗に比例します。一方、電圧は定格電圧で固定され、抵抗も定数なので、電力は電流に比例します。…ということは、銅損は電力の2乗に比例するということができます。
ここで、問題文より全負荷(300kW)のときの銅損が2800[W]です。銅損は電力の2乗で表すことができるため、全負荷時の銅損をP300とし、負荷80W、60W、40W、20Wの銅損をそれぞれP80、P60、P40、P20とすると上図右側で示したような式が書けます。
あとはそれぞれの負荷に該当する時間を掛ければ、1日の銅損P銅を求めることができます。
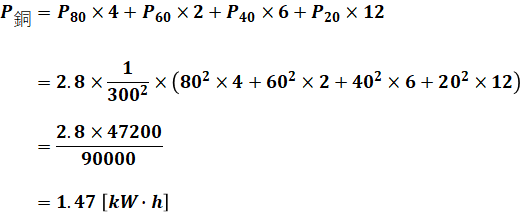
以上から、求める損失電力量は鉄損と銅損の和なので、
![]()
となり、正解は(2)だとわかります。
(b)
変圧器の全日効率というのは、「1日の間に変圧器に入力した電力量」に対する「出力された電力量」の値をいい、次の式で表すことができます。
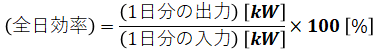
ただし、入力というのは出力と損失電力量を合わせたものなので、上式は下式のようにも書けます。

よって、これに数値を代入して計算すれば答えが得られます。
ここで、損失電力量については(a)の答えをそのまま使うことができます。一方で、出力については下図のように計算することができます(数式以外は(a)の解説と同じ図です)。
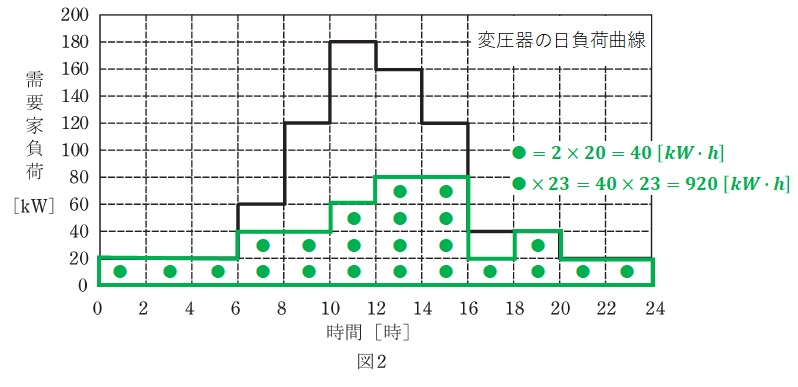
以上から、全日効率は以下のように計算できます。
![]()
よって、正解は(3)です。

コメント