電験三種 H30年 法規 問12 問題と解説

　問 題　　　　　

図のように電源側S点から負荷点Aを経由して負荷点Bに至る線路長L[km]の三相3線式配電線路があり、A点、B点で図に示す負荷電流が流れているとする。

S点の線間電圧を6600V、配電線路の1線当たりの抵抗を0.32Ω/km、リアクタンスを0.2Ω/kmとするとき、次の(a)及び(b)の問に答えよ。

ただし、計算においてはS点、A点及びB点における電圧の位相差が十分小さいとの仮定に基づき適切な近似式を用いるものとする。

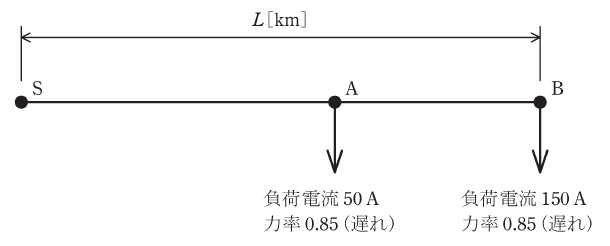
(a)　A-B間の線間電圧降下をS点線間電圧の1%としたい。このときのA-B間の線路長の値[km]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.39
2. 0.67
3. 0.75
4. 1.17
5. 1.30

(b)　A-B間の線間電圧降下をS点線間電圧の1%とし、B点線間電圧をS点線間電圧の96%としたときの線路長Lの値[km]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 2.19
2. 2.44
3. 2.67
4. 3.79
5. 4.22

 

 

 

 

 

　解 説　　　　

(a)

A-B間の線間電圧降下をS点線間電圧の1%としたいとのことですが、S点線間電圧は6600[V]なので、A-B間の線間電圧降下V_dは66[V]となります。

ここで、三相3線式電線の電圧降下V_dは以下の式を使って表すことができます。

今回の問題では、IはA-B間を流れる電流ですが、この電流はそのまま点Bの下へと進む電流なので、150[A]です。また、力率0.85ということなので、cosθ=0.85となります。ちなみに、cosθがわかっていれば、以下のようにsinθを計算することができます。

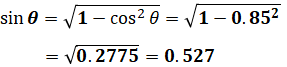
さらに、抵抗rとリアクタンスxは1kmあたりの数値[Ω/km]で与えられているため、これを[Ω]に直すにはA-B間の線路長L_ABを掛ける必要があります。

以上から、(1)式に各種の数値を代入すると以下のようになります。

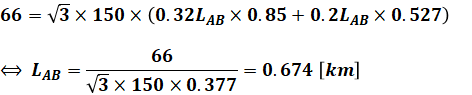
よって、正解は(2)です。

(b)

B点の電圧がS点の96%ということは、

と計算できるので、B点の電圧は6336[V]となり、S-B間の線間電圧降下は

となります。

また、(b)は(a)と同様にA-B間の線間電圧降下がS点線間電圧の1%なので、(a)での計算結果をそのまま使うことができます。

ここで、問題の図に以上のことを追記すると、以下の図のように描けます。

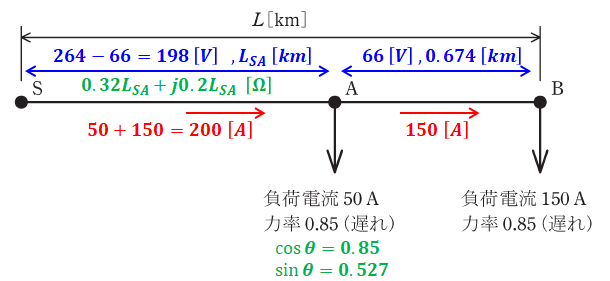
よって、上図S-A間で(a)のときと同様に(1)式を使って電圧降下の式を組み立てると、S-A間の線路長L_SAを求めることができます。

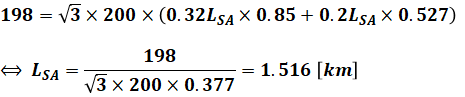
以上から、線路長Lは次のように計算できます。

よって、正解は(1)となります。