問 題
演算増幅器を用いた回路について、次の(a)及び(b)の問に答えよ。
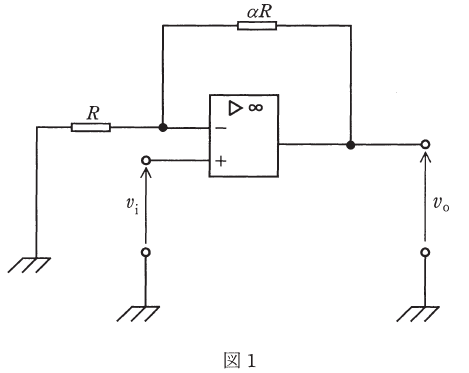
(a) 図1の回路の電圧増幅度![]() を3とするためには、αをいくらにする必要があるか。αの値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
を3とするためには、αをいくらにする必要があるか。αの値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.3
- 0.5
- 1
- 2
- 3
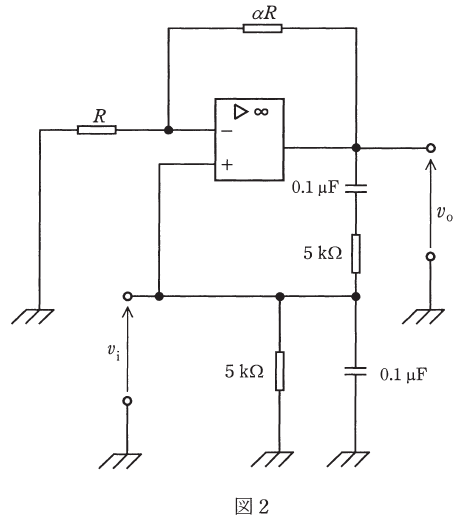
(b) 図2の回路は、図1の回路に、帰還回路として2個の5kΩの抵抗と2個の0.1μFのコンデンサを追加した発振回路である。発振の条件を用いて発振周波数の値f[kHz]を求め、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.2
- 0.3
- 0.5
- 2
- 3
解 説
(a)
まず、演算増幅器は入力インピーダンスが非常に大きいので、-端子に電流が流入せず、+端子と-端子の電圧は等しくなります。
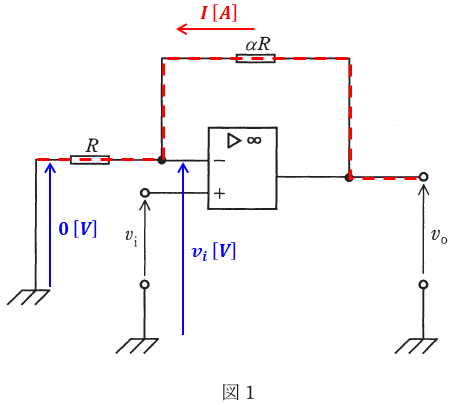
よって、上図の赤線のように電流が流れるので、その部分だけを抜き出すと以下のように描くことができます。
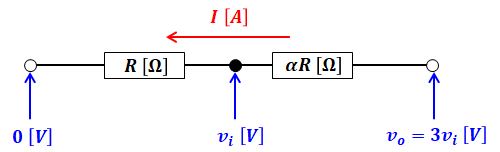
上図の0[V]からvi[V]までの範囲でオームの法則を使うと次のような式となり、
![]()
これを上図の0[V]からvo[V]までの範囲でのオームの法則の式に代入すると、以下のようにαを計算することができます。
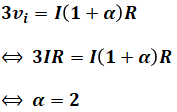
(b)
(b)はハイレベルな内容となっていて、難易度の高さや出題頻度の低さの割に点数はほかと同様5点なので、個人的にはこの問題は捨て問題としてしまっても構わないと思います。
ただし、その場合でも(a)は重要事項かつ頻出なので、(a)の解法はきちんと身につけておくことをおすすめします。
問題の図2は図1の演算増幅器に帰還回路を追加したものですが、問題文によるとこの帰還回路の追加によって、元々の回路と帰還回路とが発振するとのことです。
発振というのは、増幅回路の入力信号と帰還回路に帰還される信号とが同位相であるときに、互いの回路の働きによって増幅度がさらに増大する現象のことをいい、このような回路を増幅回路と呼んでいます。
つまり、ポイントとなるのは入力信号と帰還信号が同位相であるということです。ちなみに、元の増幅回路には抵抗しかなく(コンデンサがないので)位相は0です。
よって、帰還信号の位相も0であるべきなので、解法の方向性としては、帰還信号を式(複素数)で表し、その虚数部の係数が0になるような周波数fを求めることになります。
帰還信号の流れは以下の図の赤線であり、帰還信号の電圧はviとなります。
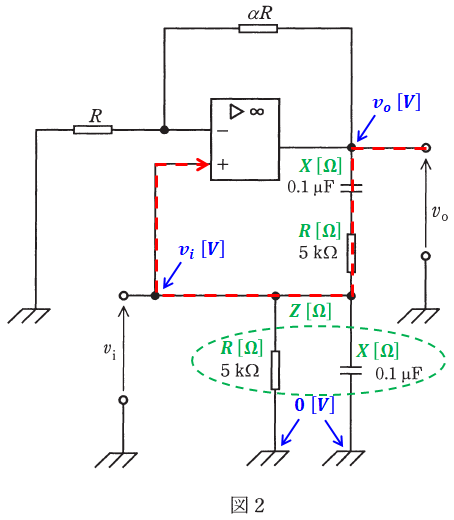
また、このviの位相は、追加された抵抗とコンデンサの位置から求めることができます。
上図の緑色で描いたように、抵抗をR、コンデンサのリアクタンスをXとし、下部の並列に並んだRとXの合成インピーダンスをZとします。すると、0[V]とvo[V]の間にZ、R、Xが直列に並ぶことになり、vi[V]はそのうちZとRの間の位置の電圧になります。
よって、viを式にすると次のようになります。
![]()
また、上記の通り帰還信号の電圧viの位相が0であることがポイントになりますが、上式のうちvoはその位相が0なので、( )内の部分の虚数部の係数が0であればよいことになります。
つまり、以下のように計算を進めることができます。
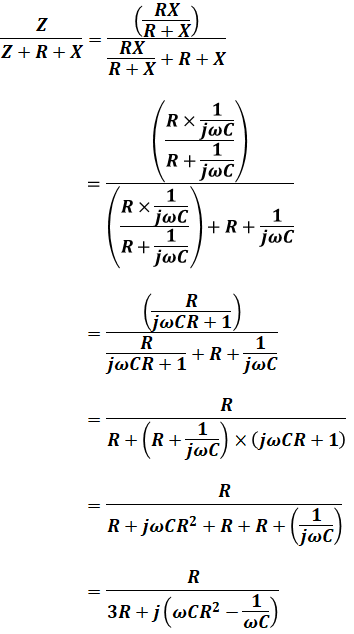
ここで、計算結果が実数になるためには、分母に含まれる虚数部の係数が0であればよいので、次のように計算を行うことで、求めるfを導出することができます。
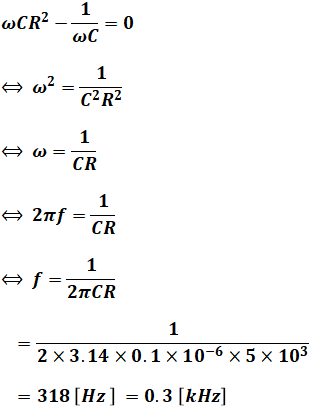

コメント