問 題
巻数Nのコイルを巻いた鉄心1と、空隙(エアギャップ)を隔てて置かれた鉄心2からなる図1のような磁気回路がある。この二つの鉄心の比透磁率はそれぞれμr1=2000、μr2=1000であり、それらの磁路の平均の長さはそれぞれl1=200mm、l2=98mm、空隙長はδ=1mmである。
ただし、鉄心1及び鉄心2のいずれの断面も同じ形状とし、磁束は断面内で一様で、漏れ磁束や空隙における磁束の広がりはないものとする。このとき、次の(a)及び(b)の問に答えよ。
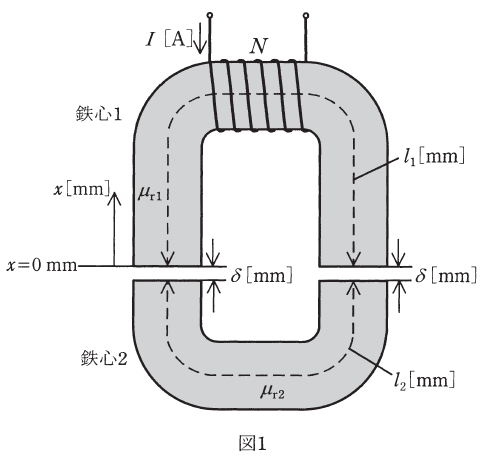
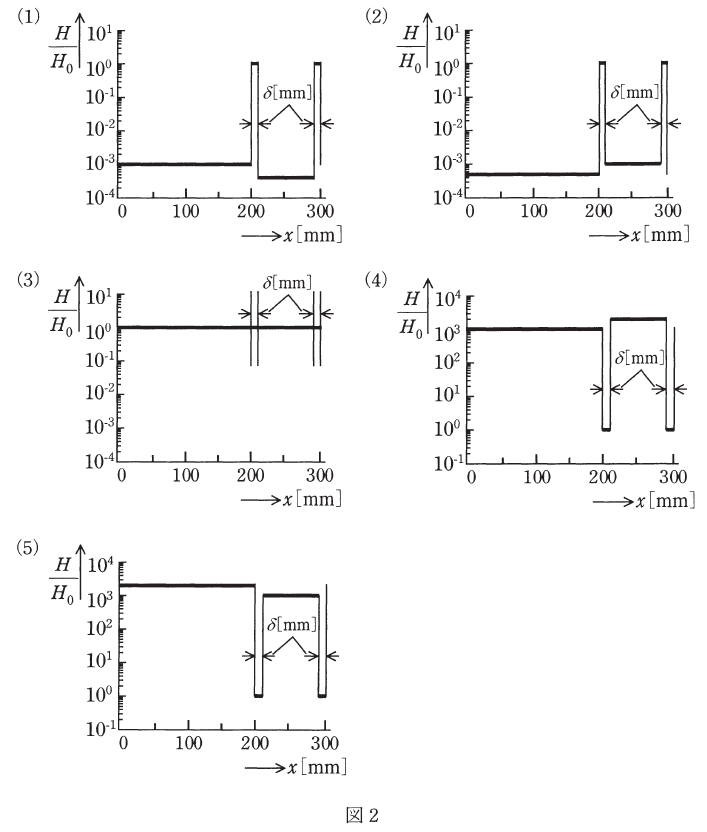
(a) 空隙における磁界の強さH0に対する磁路に沿った磁界の強さHの比
を表すおおよその図として、最も近いものを図2の(1)～(5)のうちから一つ選べ。ただし、図1に示すx=0mmから時計回りに磁路を進む距離をx[mm]とする。また、図2は片対数グラフであり、空隙長δ[mm]は実際より大きく表示している。
(b) コイルに電流I=1Aを流すとき、空隙における磁界の強さH0を2×104A/m以上とするのに必要なコイルの最小巻数Nの値として、最も近いものを次の(1)～(5)のうちから一つ選べ。
- 24
- 44
- 240
- 4400
- 40400
解 説
(a)
解説を始める前に確認しておきたいことがあります。選択肢を見ると、どれも横軸の200～300mmあたりのところが山のような形になっていますが、これは磁界の強さHを表す線とは何も関係がありません。
あくまで、x=200～201のところと、x=299～300のところは幅が太く描いてあるけれど、実際にはδ(=1mm)ですよ…と教えてくれているだけです。つまり、ここはあまり気にせず、本質的なHは太線で表されている部分だと考えてください。
それでは、解説を始めます。
磁界の強さHは「鉄心1」、「鉄心2」、「空隙」の3つのエリアでその強さが異なりますが、最もわかりやすいのは「空隙」です。
求めたいのは「空隙における磁界の強さH0に対する磁路に沿った磁界の強さHの比」ですが、「空隙」においては比較する基準も比較する対象も同じなので、当然、その比は1となります。
よって、x=200～201、299～300の範囲では、H/H0の値は1となります。選択肢の図でははっきり「1」と書いてありませんが、「100」が1のことなので、上記の範囲ではこの高さに太線が引いてあるものが正解です。
そうして選択肢をみると、(1)～(5)の全てがこの条件を満たしているので、ここでは選択肢を絞ることはできませんでした。
続いて、「鉄心1」と「鉄心2」について考えます。
透磁率μ[H/m]というのは、磁束密度B[T]と磁界の強さH[A/m]とを結ぶ式の比例定数です。
今回は比透磁率が使われていますが、これも同じような使い方ができるものです。
(以下、比透磁率の説明をするため、ちょっと脱線します。)
透磁率は磁束が通っている物質の種類によって異なります。一般的には真空の透磁率にはμ0という記号を用い、それ以外の物質では単にμとするか、必要に応じた記号をμの右下に付けます(μ1、μAなど)。
そして、真空の透磁率μ0に対するある物質の透磁率μの比を、比透磁率μrといいます。
今回の問題では、鉄心部分と空隙部分の比が問われているので、透磁率の比も比透磁率の比も一緒なので、真空の透磁率まで考慮する必要はありません。
(脱線おわり)
脱線する前に示した
という式より、磁束密度Bが変わらなければ、透磁率(比透磁率)μと磁界の密度Hは反比例することがわかります。
よって、鉄心1ではμr1=2000なので、このときのHはH0(空隙)と比べて2000分の1となり、鉄心2ではμr2=1000なので、このときのHはH0(空隙)と比べて1000分の1となります。
なので、求めるグラフは選択肢(2)が正しいです。
(b)
(b)を解く前に、問題からはちょっと話が逸れますが、重要事項として「環境コイルによる磁界の強さ」について確認しておきます。
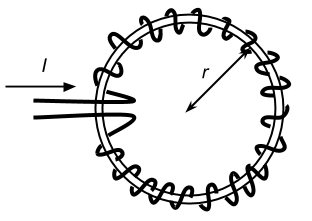
上図のような環状コイルがあったとき、この環状コイルを流れる電流がつくる磁界の強さHは、以下の式で表されます。
- H：磁界の強さ[A/m]
- N：巻き数
- I：電流[A]
- r：環状コイルの半径[m]
この式からわかるように、このコイルを流れる電流の総量(=NI)は、磁界の強さHとコイルの円周(=2πr)の積に等しくなります。
同様に、上記のように円ではなくても、閉回路における磁界の強さと閉回路の周の長さの積は、電流と等しくなるという性質があります。このルールを「アンペアの周回積分の法則」と呼びます(名前を覚える必要はありませんが…)。
以上を踏まえて、今回の問題について考えます。
今回は磁界の強さが一定ではなく、(a)で求めたように「鉄心1」、「鉄心2」、「空隙」の3パターンに分かれています。よって、それぞれの領域について磁界の強さと長さの積を求め、それらの合計が電流の総量と等しくなると考えます。
つまり、以下のような等式が成り立ちます。
- N：巻き数
- I：電流[A]
- H1、H2、H0：鉄心1、鉄心2、空隙における磁界の強さ[A/m]
- l1、l2、l0：鉄心1、鉄心2、空隙における長さ[m]
上式の各記号に数値を代入し、Nについて解くと以下のようになります(空隙の部分は、1mmが2か所あるので、計2mmとして計算しています)。
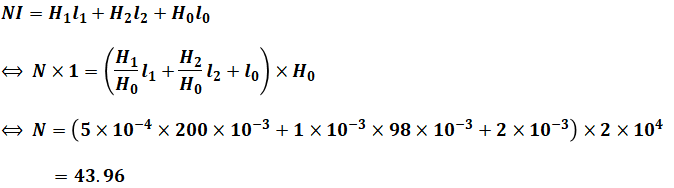
よって、43.96以上で最も小さい整数が答えなので、選択肢(2)の44が正解となります。
コメント