電験三種 H29年 機械 問17 問題と解説

　問 題　　　　　

均等拡散面とみなせる半径0.3mの円板光源がある。円板光源の厚さは無視できるものとし、円板光源の片面のみが発光する。円板光源中心における法線方向の光度I₀は2000cdであり、鉛直角θ方向の光度I_θはI_θ=I₀cosθで与えられる。また、円板光源の全光束F[lm]はF=πI₀で与えられるものとする。

次の(a)及び(b)の問に答えよ。

(a)　図1に示すように、この円板光源を部屋の天井面に取り付け、床面を照らす方向で部屋の照明を行った。床面B点における水平面照度の値[lx]とB点から円板光源の中心を見たときの輝度の値[cd/m²]として、最も近い値の組合せを次の(1)～(5)のうちから一つ選べ。

ただし、この部屋にはこの円板光源以外に光源はなく、天井、床、壁など、周囲からの反射光の影響はないものとする。

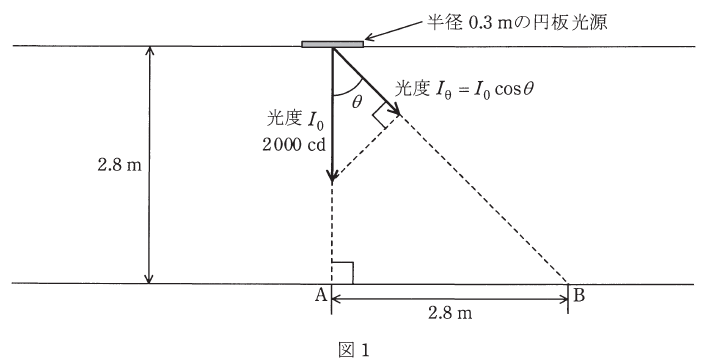
水平面照度[lx]　輝度[cd/m²]

1. 64　　　　5000
2. 64　　　　7080
3. 90　　　　1060
4. 90　　　　1770
5. 255　　　 7080

(b)　次に、図2に示すように、建物内を真っすぐ長く延びる廊下を考える。この廊下の天井面には上記円板光源が等間隔で連続的に取り付けられ、照明に供されている。廊下の長さは円板光源の取り付け間隔に比して十分に大きいものとする。

廊下の床面に対する照明率を0.3、円板光源の保守率を0.7としたとき、廊下床面の平均照度の値[lx]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

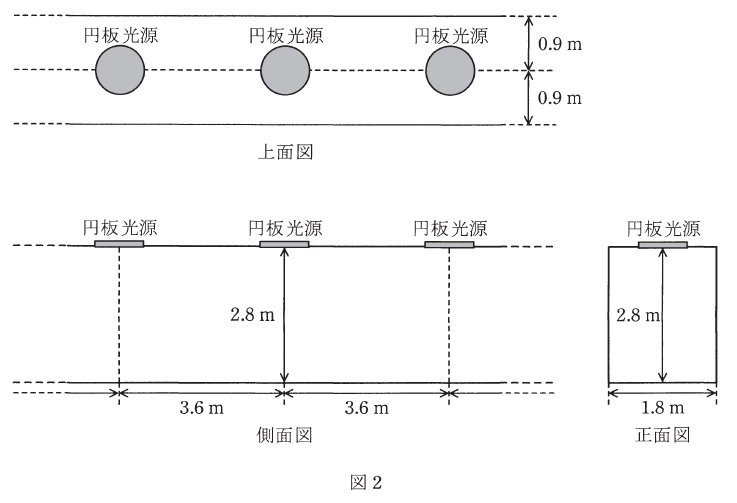
1. 102
2. 204
3. 262
4. 415
5. 2261

 

 

 

 

 

　解 説　　　　

(a)

水平面照度Eと光度I_θの関係式は以下のように表すことができます。

• E：水平面照度 [lx]
• I_θ：光度 [cd]
• r：点光源と観測点との距離 [m]
• θ：点光源の直下方向と観測点とのなす角

まず、I_θは問題文に式が与えられているので、その通り計算します。角θは未知数ですが、これは直角二等辺三角形なので、θ=π/4(45°)とわかります。

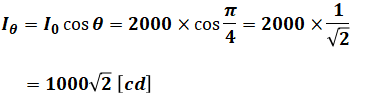
一方、距離rは直角二等辺三角形の三角比1：1：√2を使えば(または三平方の定理でも可)、斜辺であるrを計算することができます。

よって、以下の式のように計算することで、Eを求めることができます。

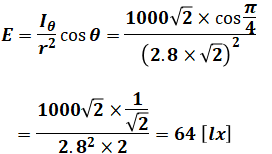
続いて輝度を求めますが、問題文に載っている単位[cd/m²]を見てもわかるように、輝度は光度を面積(光源の面積)で割ったものとなります。

ただし、光源は真下から見上げるときと斜めから見るときでは、その面積も変わってきます(極端な話、円盤光源を真横から見ると面積は0です)。つまり、問題文に載っている「鉛直角θ方向の光度I_θはI_θ=I₀cosθ」と同様に、鉛直角θ方向の光源の面積A_θは、A_θ=A₀cosθとなります。

よって、輝度Lの計算は次のようになります。

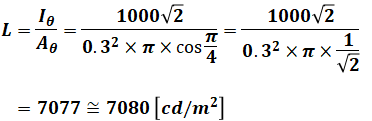
以上から、(a)は(2)が正解です。

(b)

(a)ではある1点の観測地点での照度をテーマとしていましたが、(b)では床面全体の平均照度がテーマとなっています。この場合、(a)のように照度を光度や距離を使って表すのではなく、照明率や保守率を使った別の式で平均照度を表すことができます。

• E：平均照度 [lx]
• F：光束 [lm]
• N：照明の数
• U：照明率
• M：保守率
• A：面積 [m²]

上式の一部分「E=F/A」を見てわかるように、照度Eは光束Fを面積Aで割ったものともいえます。照度は実際に生活したり作業したりするときの部屋の明るさを示す指標となり、光源の光束が強いほど明るく、一方で照らす面が広いと暗く感じます。

また、実際には部屋に照明器具が複数あるのが普通なので、その個数がNです。

そして、照明の光の一部は壁や床などに吸収されたり、窓の外へ抜けていったりして、作業面を照らすという役割を持ちません。照明率Uというのは、全ての光束のうち、照らしたい場所を照らすのに役立っている光束の割合を意味します。

さらに、照明は新品の状態では充分に明るさが確保できるものですが、時間が経って古くなってくると照明器具の劣化や汚れなどにより、充分な明るさが確保できない場合があります。そのため、このような理由で不足してしまう明るさを初めから考慮に入れておくのが保守率Mの考え方です。

よって、この問題では、上式の右辺を計算するために、光束F、照明の数N、照明率U、保守率M、面積Aの値を知ることが求められます。

まず、光束Fについて。

光束Fは光度Iと立体角ωの積で表すことができます。

立体角ωというのは、ある点からの空間的な広がりを表す変数で、次の式で表されます。

• ω：立体角 [sr]
• S：光源の表面積 [m²]
• r：光源の中心から表面までの距離 [m]

今回は光源が円板光源なので、ωは次のように計算できます。

よって、光束Fは以下のように求めることができます。

続いて、照明の数Nについて。

これは問題文にはいくつと明記されていませんが、照明が等間隔に並んでいるので、とりあえず照明の数は1つであると考えて、廊下の面積Aも照明1つが照らす分だけにして考えればよいので、とりあえずN=1として話を進めます(必ずしもN=1にしなくてもよいですが、Nを増やす分だけ面積Aも大きくする必要があります)。

また、照明率U、保守率Mについては問題文に数値が与えられているので、それをそのまま使うことができます。

最後、面積Aについて。

上記の通り、照明1つ分が照らす必要のある面積について考えます。これは図2の上側を使うとわかりやすいので、以下に再度示します。

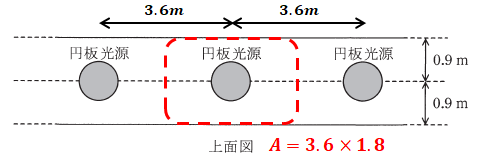
上図のように、光源同士の距離は3.6mなので、1つの光源が照らすべき範囲は、左右に1.8mずつ、計3.6mとなります。また、廊下の幅は1.8mなので、面積Aは

となります。

以上で求めた各種の数値を最初の式に示した平均照度Eの式に代入すると、

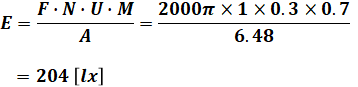
となって、正解が(2)であることがわかります。