問 題
図1に示す単相交流電力調整回路が制御遅れ角α[rad]で運転しているときの動作を考える。
正弦波の交流電源電圧はvS、負荷は純抵抗負荷又は誘導性負荷であり、負荷電圧をvL、負荷電流をiLとする。次の(a)及び(b)の問に答えよ。
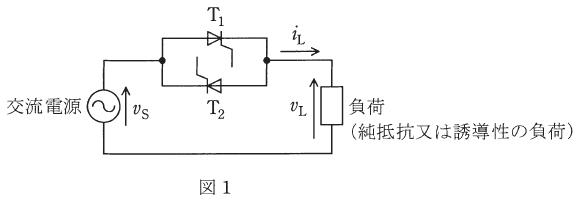
(a) 図2の波形1～3のうち、純抵抗負荷の場合と誘導性負荷の場合とで発生する波形の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。
純抵抗負荷 誘導性負荷
- 波形1 波形2
- 波形1 波形3
- 波形2 波形1
- 波形2 波形3
- 波形3 波形2
(b) 交流電源電圧vSの実効値をVSとして、純抵抗負荷の場合の負荷電圧vLの実効値VLは、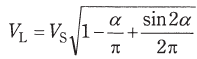
で表される。
制御遅れ角を
から
に変えたときに、負荷の抵抗で消費される交流電力は何倍となるか、最も近いものを次の(1)～(5)のうちから一つ選べ。
- 0.550
- 0.742
- 1.35
- 1.82
- 2.00
解 説
(a)
(a)の解説の前に言葉の確認をしておきますが、純抵抗負荷というのは抵抗だけの負荷のことで、有効電力だけを消費する(=力率1)負荷です。また、誘導性負荷は、抵抗のほかにコイルの誘導性リアクタンスを含む負荷で、力率は「遅れ」となります。
ちなみに、この問題では余談ですが、容量性負荷は、抵抗とコンデンサの容量性リアクタンスをもった負荷で、力率は「進み」となります。
ここで、純抵抗負荷の場合から考えます。
図2の波形1～3のvSは全て同じかたちをしているので、これが軸になります。
vSの位相をθとすると、0≦θ≦πの範囲ではvSは正なので、電流は図1のサイリスタT1側を左から右へと流れ、π≦θ≦2πの範囲ではvSは負なので、電流はサイリスタT2側を右から左へと流れます。
ただし、制御遅れ角αにより、θ=αになるまではターンオンしないため、0≦θ≦αの範囲ではvLに電圧は生じません。
ターンオン(vSの位相θが制御角αになるとき)からターンオフ(vSが0になるとき、つまりθ=π)までの間は、vLがvSと連動した値をとります。
また、π≦θ≦2πの範囲でも同様のことが反対向きに行われるので、これらをまとめると以下のようになります。
- 0≦θ≦α ：vL=0(まだターンオンしていない)
- α≦θ≦π ：vL=vS(αでターンオン、πでターンオフ)
- π≦θ≦π+α ：vL=0(まだターンオンしていない)
- π+α≦θ≦2π：vL=vS(π+αでターンオン、2πでターンオフ)
以上を満たすvLの波形は波形1なので、純抵抗負荷は波形1となります。また、純抵抗負荷は抵抗のみ(力率1)なので、負荷の電圧vLと電流iLの位相は一致します。波形1はこの点も矛盾がないので、やはり正しいということになります。
続いて、誘導性負荷の場合を考えます。
こちらも純抵抗負荷のときと大きく異なることはありませんが、負荷の力率が「遅れ」になっていることから、θ=πでvS=0となったあともリアクタンスに蓄えられたエネルギーを放出している間は電流が流れ続け、本来のターンオフのタイミング(θ=π)から少し遅れてターンオフします。
ちなみに、このようにターンオフのタイミングは変わりますが、ターンオン時は電源側からエネルギーが供給されているので、ターンオンのタイミングは変わりません(θ=α、θ=π+α)。あくまで、電源側から供給されなくなった時点(=ターンオフ)でリアクタンスのエネルギーを放出しだすと考えてください。
よって、誘導性負荷のvLの波形は、純抵抗負荷のvLの波形と比べて、ターンオンが一緒でターンオフが遅れるので、波形2または波形3となります。
ここで、誘導性負荷は力率が1ではないので、負荷の電圧vLと電流iLの位相は一致せず、また、vS=0となった瞬間からリアクタンスのエネルギーを放出するのに伴い電流が流れることを加味すると、波形3のようにvLとiLがきれいに連動することはありません。
よって、波形2が正しいということになります。
以上から、(a)の正解は(1)です。
(b)
(b)ではαが変化したときの電力の変化率が問われています。
電力Pを求める式は、電圧V、電流I、抵抗Rのいずれか2つを使って表すことができますが、ここではVとRを使って、
と表します。というのも、電圧は問題文で式として与えられていて、また、抵抗は制御角が変わっても不変の値をとるからです。
一方、電流は(a)で見てきた波形1からもわかるように、位相によって変化するので、電流の実効値を求めるのはかなり複雑になります。
ここまでわかれば、あとは問題文で与えられた式や数値を使いながら、電力の比の計算をひたすら進めていくことになります。
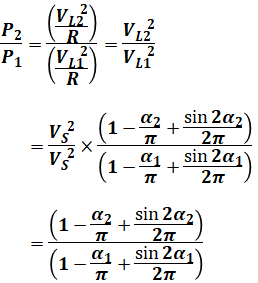
ちなみに、上式のP、VLの右下に1とか2と付けたのは、問題文のα1、α2と合わせています。
一方でVSには1や2を付けていませんが、これはVSが電源電圧の実効値であり負荷側の数値ではないので、制御遅れ角αが変わっても同じ値のままだからです。そのため、VS/VSはそのまま約分して消すことができます。
上式のαに数値を代入して計算を進めると、以下のようになります。
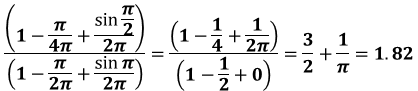
コメント