問 題
定格容量50kV・Aの単相変圧器において、力率1の負荷で全負荷運転したときに、銅損が1000W、鉄損が250Wとなった。力率1を維持したまま負荷を調整し、最大効率となる条件で運転した。
銅損と鉄損以外の損失は無視できるものとし、この最大効率となる条件での効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 95.2
- 96.0
- 97.6
- 98.0
- 99.0
解 説
変圧器の損失には、負荷を掛けているときに生じる損失(負荷損=銅損)と、負荷があってもなくても発生する損失(無負荷損=鉄損)との2種類があります。
負荷損というのは銅損のことで(厳密には違いますが、電験三種の範囲では同じものと見なせます)、銅は電気を通しやすいので導線に使われるため、通電中に生じる損失だと覚えればよいと思います。また、銅損の大きさは負荷を流れる電流の2乗に比例します。
一方、無負荷損は鉄損のことで、鉄はコイルの鉄心などに使われていて、電流の有無に関わらず磁気は生じていることから、電流に関わらず損失が生まれると考えてください。鉄損の場合は、電流の大きさに関わらず、損失は一定の値をとります。
上記を踏まえてここからが本題ですが、電流を流せば流すほど出力は上がりますが、一方で銅損も大きくなってしまいます。
入力電力は電流に比例しますが、銅損は電流の2乗に比例して大きくなるため、出力の効率が最も良いときは、入力が増えるメリットと銅損が増えるデメリットのちょうどバランスが取れたところということになります。
そして、最も効率の良いときの電流の大きさは、「鉄損=銅損」となるときの電流値です。
このことは式を使って証明することもできますが、結論だけを覚えておけば充分だと思いますので、ここでは割愛します。鉄損と銅損が同じ値をとるとき、変圧器の効率が最大となることを重要事項として覚えておいてください。
よって、今回の問題では鉄損が250Wなので、銅損も250Wにすることが求められます。
ここで、全負荷運転では銅損が1000Wなので、銅損を250Wにするには銅損を全負荷時の1/4にすればよいです。また、銅損は電流の2乗に比例するため、これを1/4にしたければ、電流を1/2にすることになります。
定格電圧は一定なので、電流を半分にするというのは負荷を半分にするということです。つまり、この変圧器の場合は、負荷率がちょうど50%のときに、その効率が最大となります。
よって、最大効率ηは、以下の式のように計算することで求めることができます。
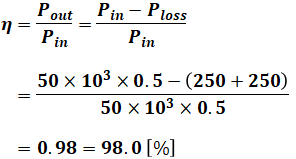
- η:効率
- Pin:入力(今回は定格容量の50%)
- Pout:出力
- Ploss:損失(鉄損+銅損の和)
以上から、正解は(4)となります。

コメント