問 題
次の文章は、一般的な電気機器(変圧器、直流機、誘導機、同期機)の共通点に関する記述である。
- ( ア )と( イ )は、磁束の大きさ一定、電源電圧(交流機では周波数も)一定のとき回転速度の変化でトルクが変化する。
- 一次巻線に負荷電流と励磁電流を重畳して流す( イ )と( ウ )は、特性計算に用いる等価回路がよく似ている。
- 負荷電流が電機子巻線を流れる( ア )と( エ )は、界磁磁束と電機子反作用磁束のベクトル和の磁束に比例する誘導起電力が発生する。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ)
- 誘導機 直流機 変圧器 同期機
- 同期機 直流機 変圧器 誘導機
- 直流機 誘導機 変圧器 同期機
- 同期機 直流機 誘導機 変圧器
- 直流機 誘導機 同期機 変圧器
解 説
aの文章では( ア )と( イ )が並列に並んでいますが、ここには直流機、誘導機、同期機のうち2つが入ります(変圧器は回転体ではないので除外)。
直流機のトルクの式は以下の通りで、磁束と電機子電流に比例します。
- T：トルク[N・m]
- k：比例定数
- Φ：磁束[Wb]
- I：電機子電流[A]
また、電機子電流Iは問1で解説した通り、以下の式で表されるので、Iの値が変われば逆起電力Eも変化します(下の式に馴染みがない場合は、問1の解説に載せた回路図を参照してください)。
- E：逆起電力[V]
- V：電源電圧[V]
- I：電流[A]
- Ra：電機子巻線抵抗[Ω]
さらに、Eは次式で表され、回転速度nに比例します。
- E：逆起電力[V]
- k’：比例定数
- Φ：磁束[Wb]
- n：電機子の回転速度[min-1]
以上から、回転速度が変われば電圧が変化し、それによって電流も変わり、さらにはトルクも変化するため、直流機は( ア )か( イ )に入ります。
続いて、誘導機について考えます。
誘導機の二次入力P2はトルクTと同期角速度ωの積で表されるため、トルクについて解くと次のようになります。
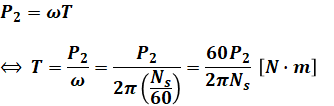
- P2：二次入力[W]
- ω：同期角速度[rad/s]
- T：トルク[N・m]
- Ns：同期速度[min-1]
さらに、同期速度Nsと回転速度Nは、滑りsを使うと以下の等式で表すことができます。
よって、回転速度の変化でトルクが変化するため、誘導機も( ア )か( イ )に入ります。
そうなると、残る同期機はトルクと回転速度が連動しないことになりますが、一応確認しておきます。
同期機はその名の通り、回転速度が同期速度と同じになる(=同期する)のが特徴です。よって、同期機の回転速度を変化させること自体がやや違和感のある(同期しなくなってしまう)ことなので、aに文章は同期機に当てはまるような内容ではありません。
ちなみに、同期機のトルクの式は以下のように表すことができ、トルクはsinδに比例します。
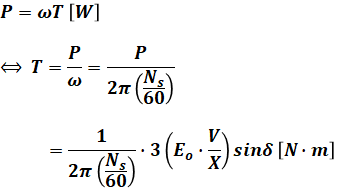
- P：三相同期機の出力[W]
- T：トルク[N・m]
- Ns：同期速度[min-1]
- Eo：内部誘導起電力[V]
- V：電機子端子電圧[V]
- X：同期リアクタンス[Ω]
- δ：EoとVとの位相角[rad]
bに関して、等価回路が似ているのは誘導機と変圧器です。その等価回路は次のように描くことができます。
よって、( イ )と( ウ )には誘導機と変圧器が入るので、aの文章と合わせると、( ア )が「直流機」、( イ )が「誘導機」、( ウ )が「変圧器」となり、選択肢(3)が正解だとわかります。
すでに答えは確定していますが、cについても確認していきます。
誘導起電力が磁束に比例するのは、直流機と同期機です。直流機の誘導起電力の式はaの解説のところでも載せましたが、以下の通りです。
- E：逆起電力[V]
- k：比例定数
- Φ：磁束[Wb]
- n：電機子の回転速度[min-1]
また、同期機の誘導起電力の式は次のようになります。
- Eo：内部誘導起電力[V]
- k：巻線係数f：周波数[Hz]
- w：巻数(1相あたり)
- Φ：磁束[Wb](1極あたり)
よって、どちらも誘導起電力が磁束に比例するため、( ア )と( エ )には直流機と同期機が入るので、正解は(3)となります。
コメント