問 題
定格出力10MV・A、定格電圧6.6kV、百分率同期インピーダンス80%の三相同期発電機がある。
三相短絡電流700Aを流すのに必要な界磁電流が50Aである場合、この発電機の定格電圧に等しい無負荷端子電圧を発生させるのに必要な界磁電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、百分率同期インピーダンスの抵抗分は無視できるものとする。
- 50.0
- 62.5
- 78.1
- 86.6
- 135.3
解 説
以下に示すのは、同期発電機の特性を示す無負荷飽和曲線と短絡曲線です。
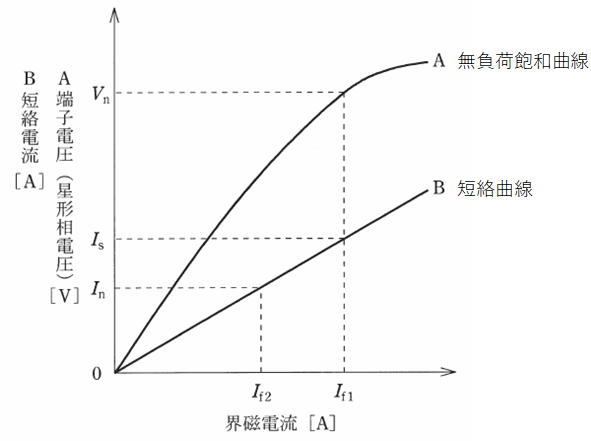
無負荷飽和曲線は、同期発電機を定格速度で運転し、界磁電流を0から徐々に増加させたときの端子電圧と界磁電流との関係を表した曲線のことをいいます。
図を見てもわかる通り、界磁電流(横軸)が小さい範囲では、端子電圧(縦軸)は界磁電流にほぼ比例します。また、界磁電流が大きくなると端子電圧は段々と飽和していき、頭打ちとなります。
短絡曲線は、同期発電機の電機子巻線の三相の出力端子を短絡し、定格速度で運転して、界磁電流を0から徐々に増加させたときの短絡電流と界磁電流との関係を表した曲線のことをいいます(直線に見えますが一応曲線です)。
この曲線は、界磁電流(横軸)と短絡電流(縦軸)がほぼ比例の関係となる点が特徴的です。
上記を踏まえて、問題文を見ていきます。
まず、問われているのは定格電圧Vnのときの界磁電流なので、上図でいうとIf1です。
これを知るためには、界磁電流がIf1のとき(定格電圧Vnのとき)の短絡電流Isと、あとは短絡曲線上のどこか1点における界磁電流と短絡電流の両方の値がわかれば、比の計算からIf1を求めることができます。
問題文によると界磁電流50Aと短絡電流700Aの組み合わせがすでに与えられているため、当面の方向性はIsを求めることとなります。
短絡電流Isは、百分率同期インピーダンス%Zと定格電流Inを使って以下のように表すことができます。この式は重要公式として覚えておいてください。
![]()
ここで、%Zは問題文で与えられていて、Inは定格出力Pnと定格電圧Vnから以下のように計算することができます。
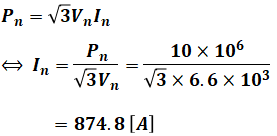
よって、これを先程の式に代入すると、
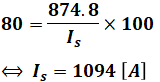
となります。
以上から、最初に示したように、界磁電流と短絡電流の組み合わせが、50Aと700A、If1と1094Aの2組できたので、比の計算によってIf1を求めることができます。
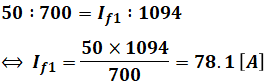

コメント