電験三種 H29年 電力 問17 問題と解説

　問題　　　　　

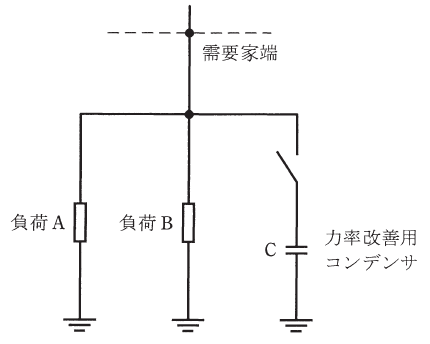
特別高圧三相3線式専用1回線で、6000kW(遅れ力率90%)の負荷Aと3000kW(遅れ力率95%)の負荷Bに受電している需要家がある。

次の(a)及び(b)の問に答えよ。

(a)　需要家全体の合成力率を100%にするために必要な力率改善用コンデンサの総容量の値[kvar]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(b)　力率改善用コンデンサの投入・開放による電圧変動を一定値に抑えるために力率改善用コンデンサを分割して設置・運用する。下図のように分割設置する力率改善用コンデンサのうちの1台(C1)は容量が1000kvarである。C1を投入したとき、投入前後の需要家端Dの電圧変動率が0.8%であった。

需要家端Dから電源側を見たパーセントインピーダンスの値[%](10MV・Aベース)として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、線路インピーダンスXはリアクタンスのみとする。また、需要家構内の線路インピーダンスは無視する。

正解 (a)-(4), (b)-(2)

　解説　　　　

負荷Aと負荷Bに含まれる無効電力の分をコンデンサCで相殺し、力率を100%に改善するという話です。よって、まずは負荷A、Bのそれぞれについて、有効電力と力率から無効電力を計算する必要があります。

有効電力P[W]、無効電力Q[var]、皮相電力S[W]、力率cosθは以下の図で表すことができます。

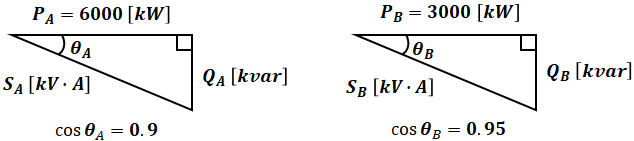
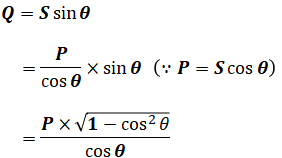
よって、Q_AとQ_Bとの和Qは次のように計算することができます(計算の方法は三角比を使ったり三平方の定理を使ったり、どのようなやり方でも構いません。以下は一例です)。

負荷の無効電力とコンデンサの容量は位相が反対なので、上記で求めた分と同じだけの容量を持つコンデンサを使えば力率が100%になるので、答えは(4)となります。

%インピーダンスと電圧変動(電圧降下)を表す式は、2つとも重要公式として覚えておきたいです。

上式は公式として暗記すればよいと思いますが、もし導出について知りたければ、%インピーダンスについては%Z(%インピーダンス)と短絡電流の計算のページを、電圧降下については三相3線式送電線の電圧降下のページを参照してください。

ここで、問題文より線路インピーダンスXはリアクタンスのみなので、%Zの式にあるZはZ=Xとなります。また、電圧降下の式ではR=0、力率0であり、sinθ=1となります。よって、上式は以下のように書き換えることができます。

上の2つの式は似ているので組み合わせると、

となります。

この関係式が意味するところは、線間電圧に対する電圧変動の比(つまり電圧変動率)を百分率で表したものが、%インピーダンスであるということです。よって、電圧変動率が0.8%なら、%インピーダンスも0.8%となります。

ただし、0.8%が答えにはなりません(選択肢にも0.8がありません)。…というのも、これは問題文で要求されている10[MV・A]ベースではないからです。今回の電圧変動はコンデンサC1を投入する前後で比較しているので、1000[kV・A]=1[MV・A]ベースの話です。

また、ここでのポイントは2つで、ひとつは、負荷Aや負荷Bの分はC1を投入する前後で変化がないので電圧変動率には関係がなく、それらのインピーダンスなどは気にしなくて大丈夫です。

もうひとつ、問題の図には1000[kvar]と書いてあるのに上記で1000[kV・A]と書けるのは、コンデンサには抵抗分がないため、リアクタンスがそのままインピーダンスになるためです。

以上から、1[MV・A]ベースでの%Zが0.8%とわかったので、求める10[MV・A]ベースでの%Zは、

となります。

電験三種 H29年電力問17 問題と解説