電験三種 H29年 電力 問16 問題と解説

　問題　　　　　

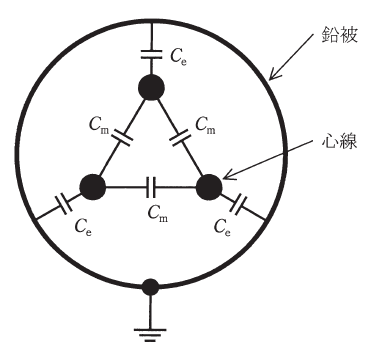
図に示すように、対地静電容量C_e[F]、線間静電容量C_m[F]からなる定格電圧E[V]の三相1回線のケーブルがある。

今、受電端を開放した状態で、送電端で三つの心線を一括してこれと大地間に定格電圧E[V]の倍の交流電圧を加えて充電すると全充電電流は90Aであった。

次に、二つの心線の受電端・送電端を接地し、受電端を開放した残りの心線と大地間に定格電圧E[V]の倍の交流電圧を送電端に加えて充電するとこの心線に流れる充電電流は45Aであった。

次の(a)及び(b)の問に答えよ。

ただし、ケーブルの鉛被は接地されているとする。また、各心線の抵抗とインダクタンスは無視するものとする。なお、定格電圧及び交流電圧の周波数は、一定の商用周波数とする。

(a)　対地静電容量C_e[F]と線間静電容量C_m[F]の比として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(b)　このケーブルの受電端を全て開放して定格の三相電圧を送電端に加えたときに1線に流れる充電電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

正解 (a)-(5), (b)-(1)

　解説　　　　

(a)を解く際のポイントは、この見慣れない図を普段見ているようなわかりやすい図に描き換えることです。

まず、最初の条件から確認していきます。

「三つの心線を一括」ということで、3つある「●」の部分は等電位となっているので、その間にあるコンデンサC_mには静電容量が一切なく、電線と同じ扱いとして問題ありません。

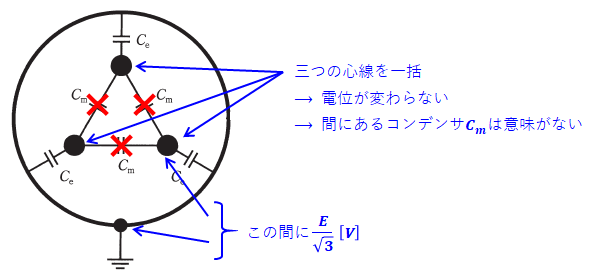
よって、上図の回路を描き換えると以下のような等価回路になります。

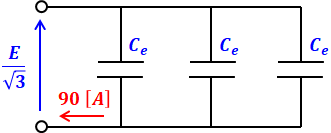
ちなみに、並列に並んだコンデンサの静電容量の合成は、それらの和によって求められるので、この場合の回路全体の静電容量は3C_eとなります。

続いて、次の「二つの心線の受電端・送電端を接地し～」の条件を考えます。

今度は3つの心線のうちの2つに対して、その受電端と送電端の両方を接地します。つまり、下図に記入したように4つのポイントで接地されていると考えることができるので、その間に挟まれた3つのコンデンサには静電容量がなく、電線と同様に扱えます。

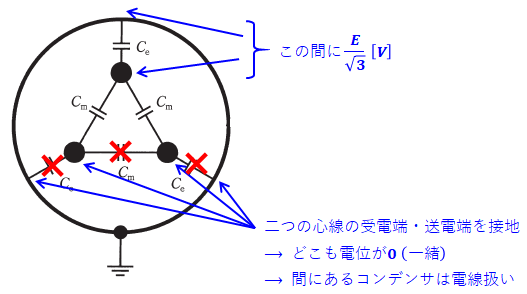
よって、上図の回路を描き換えると以下のような等価回路になります。

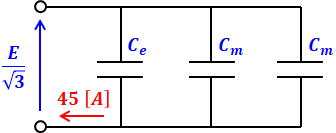
先程と同様に回路全体の静電容量を考えると、今度の場合はC_e+2C_mとなります。

ここで、求めたいのはC_e/C_mですが、今のところわかっているのは回路全体の静電容量と、そこを流れる電流です。

ですが、静電容量と電流が比例関係にあることを知っていれば、上記で求めた2つの回路の合成静電容量と問題文で与えられた電流の値から、比の計算によってC_e/C_mを求めることができます。

ちなみに、静電容量と電流が比例関係にあるというのは、以下のようなオームの法則から導くこともできます。下式より、Eとωが一定の場合、IはCに比例します。

よって、以下の比の計算によって求めるC_e/C_mを算出できます。

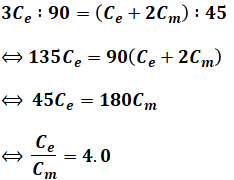
(b)を解く際には問題で与えられた図のままだと考えにくいので、(a)のときと同様、見慣れた図に描き換えることが重要です。

問題文によると、全ての受電端を開放して、1線に流れる(1相あたりの)電流値を求めたいので、今度は問題の図で消すところはなく、全てをそのまま使います。つまり、当面の目標は、問題の図から1相あたりの等価回路を描き上げることになります。

図の描き換え方法は色んなやり方がありますので、以下の通りじゃなくても構いません。一例として参考にして下さい。

まず、図を描き換えの第一手は接地の位置です。接地点からぐるっと円を描くのはあまり見慣れませんが、円周には抵抗やコンデンサがないので、円周は全て接地されていて等電位です。

そして、その円周から3つのコンデンサC_eに接続されているので、これはひとつの接地点(点oとします)から三方にコンデンサC_eが接続されているY結線と同じだと判断できます。

また、そのY結線のそれぞれの先端を点a、b、cとすると、点aと点bの間にコンデンサC_mがあって、点bと点cの間、点cと点aの間にも同様にC_mがあります。

よって、以下の図のように、Y結線のそれぞれの先端を結ぶ形でΔ結線ができているということになります。

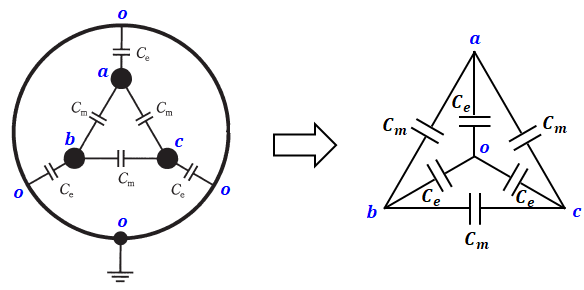
この描き換えができるかどうかが、この問題のヤマだと思います。ここまでが理解できれば、あとは基本的事項です(基本が故に、重要ですが)。

今度は上図右側の三相回路から1相を取り出したいのですが、1相を抜き出す際ためには中性点を使って架空の中性線を引きたいので、Y結線にしなければいけません。

よって、上図右側のΔ結線(3つのC_mのところ)をY結線に直しますが、Δ-Y変換の際には各コンデンサの静電容量が3倍になります(C_Y=3C_Δ)。

こうすると上図右側は下図のように描き換えることができます。

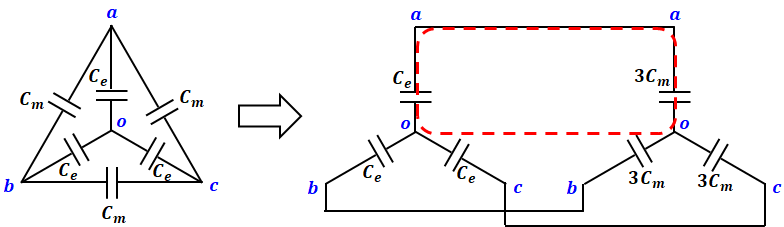
よって、上図右側の赤点線の部分が1相分になるので、その等価回路は以下のようになります。

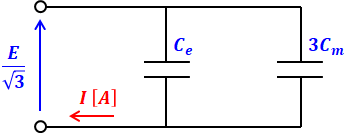
最終的に求めたいのは上図の電流Iですが、その前に、この回路の合成静電容量はC_e+3C_mとなります。

ここで、(a)で解説したように電流と静電容量は比例関係にあるため、(a)でも使った「3C_eのときに90[A]」というのと、今回のを比較すると、

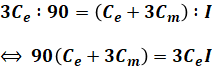
となり、(a)の解から「C_e=4C_m」なので、

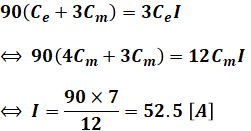
のように計算することができます。

電験三種 H29年電力問16 問題と解説