問 題
原子力発電に用いられるM[g]のウラン235を核分裂させたときに発生するエネルギーを考える。ここで想定する原子力発電所では、上記エネルギーの30%を電力量として取り出すことができるものとし、この電力量をすべて使用して、揚水式発電所で揚水できた水量は90000m3であった。
このときのMの値[g]として、最も近い値を次の(1)~(5)のうちから一つ選べ。
ただし、揚水式発電所の揚程は240m、揚水時の電動機とポンプの総合効率は84%とする。また、原子力発電所から揚水式発電所への送電で生じる損失は無視できるものとする。
なお、計算には必要に応じて次の数値を用いること。
- 核分裂時のウラン235の質量欠損 0.09%
- ウランの原子番号 92
- 真空中の光の速度 3.0×108m/s
- 0.9
- 3.1
- 7.3
- 8.7
- 10.4
正解 (5)
解 説
まず、ウランの核分裂で発生するエネルギーは以下の通りです。
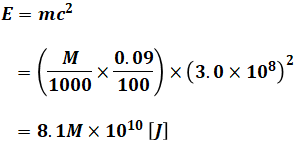
- E:エネルギー[J]
- m:核分裂で失ったウランの質量[kg]
- c:光速[m/s]
問題文より、このうちの30%を電気量として取り出せるので、原子力発電で得られるエネルギーは次のようになります。
![]()
一方、揚水を行うには、理論的には位置エネルギーの分だけ必要で、現実的にはそれに電動機効率とポンプ効率による損失分を加味することになります。
よって、揚水を行うのに消費するエネルギーは次のような計算となります。
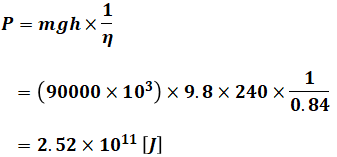
- P:揚水で使うエネルギー[J]
- m:水の質量[kg]
- g:重力加速度 9.8[m/s2]
- h:高さ(揚程)[m]
- η:電動機とポンプの総合効率
以上から、発電したエネルギーと揚水に使ったエネルギーは等しいので、以下のように計算することで、求めるMを算出できます。
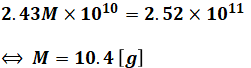

コメント