電験三種 H28年 理論 問18 問題と解説

　問題　　　　　

振幅変調について、次の(a)及び(b)の問に答えよ。

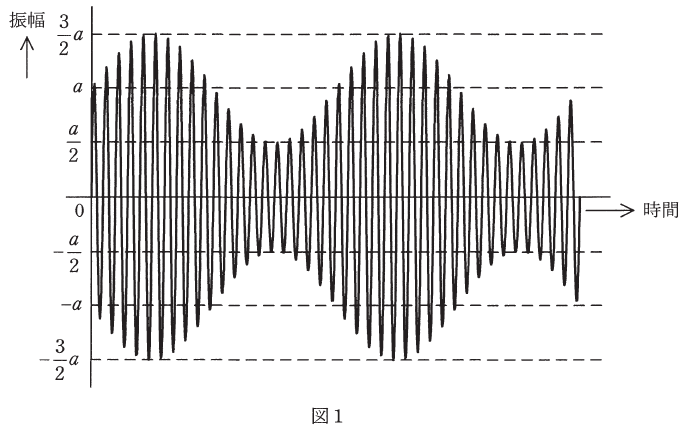
(a)　図1の波形は、正弦波である信号波によって搬送波の振幅を変化させて得られた変調波を表している。この変調波の変調度の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(b)　次の文章は、直線検波回路に関する記述である。

振幅変調した変調波の電圧を、図2の復調回路に入力して復調したい。コンデンサC[F]と抵抗R[Ω]を並列接続した合成インピーダンスの両端電圧に求められることは、信号波の成分が(　ア　)ことと、搬送波の成分が(　イ　)ことである。

そこで、合成インピーダンスの大きさは、信号波の周波数に対してほぼ抵抗R[Ω]となり、搬送波の周波数に対して十分に(　ウ　)なくてはならない。

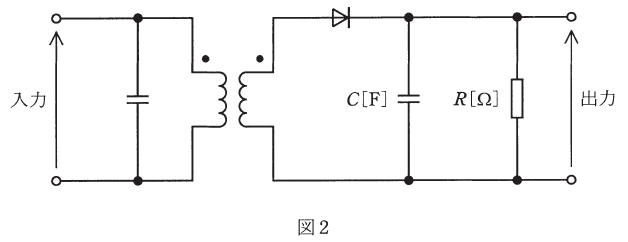
上記の記述中の空白箇所(ア)、(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

　　　(ア)　　　　　(イ)　　　(ウ)

正解 (a)-(2), (b)-(2)

　解説　　　　

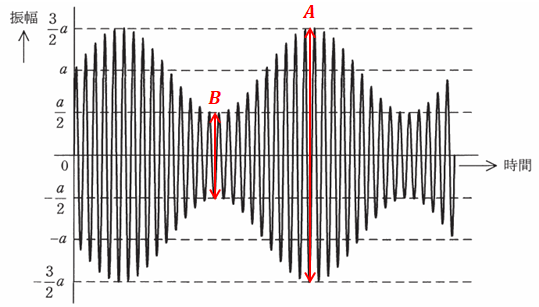
AM(振幅変調)の変調度mは、最大の振幅Aと最小の振幅Bの和に対する、それらの差で表すことができます。

ただし、ここでいう振幅とは、正から負までの幅を指します。0から正方向の片側だけではない点に注意してください。上式を見てもわかるように、変調度mは必ず1以下の値をとるため、(4)や(5)の選択肢のようになることは有り得ません。

問題の図で与えられた数値より、A=3a、B=aなので、これらを上式に代入すると、mは次のように計算できます。

よって、正解は(2)となります。

最初に信号波と搬送波の意味について確認しておきます。

(b)の問題文では復調回路がテーマになっているということは、すでにデータの送信は済んでいて、そのデータから信号波(音声データなど)を取り出したい、という流れです。搬送波はデータの送信のためには重要な要素ですが、それが済んで信号波だけを取り出したいときには不要なものです。

よって、復調回路においては信号波を残しつつ搬送波をなくさなければならないので、(　ア　)には「ある」が入り、(　イ　)には「なくなる」が入ります。

また、(b)の問題文の後半について、信号波の成分があるということは、問題の図2における抵抗Rに電流が流れ、その両端に電圧差が生じるということです(図2では「出力」という文字と矢印で表記してあるところ)。

コンデンサCのリアクタンスをX(=1/2πfC)とすると、信号波の周波数fにおいて「X≫R」となるようにRやCの値を調整すれば、コンデンサCの抵抗が大きすぎるので図2のCには電流が流れず、全てRのほうにいくので、信号波の成分が出力されることになります。

これが、問題文に記載されている「合成インピーダンスの大きさは、信号波の周波数に対してほぼ抵抗R」の意味するところです。

一方、搬送波の周波数f'(信号波の周波数fとは違う値)のときに「X≒0」となるようにCの値を調整することで、今度は図2においてコンデンサCのほうに電流が流れ、抵抗Rのほうには電流がいかなくなります。

すると、Rの両端に電圧差が発生することもないため、出力は0となり、(　イ　)で答えたような条件が実現できます。

よって、搬送波の場合は合成インピーダンスが小さいほうがよいので、(　ウ　)には「小さく」が入ります。

以上から、

となるので、正解は(2)です。

電験三種 H28年理論問18 問題と解説