問 題
図のように、r[Ω]の抵抗6個が線間電圧の大きさV[V]の対称三相電源に接続されている。b相の×印の位置で断線し、c-a相間が単相状態になったとき、次の(a)及び(b)の問に答えよ。
ただし、電源の線間電圧の大きさ及び位相は、断線によって変化しないものとする。
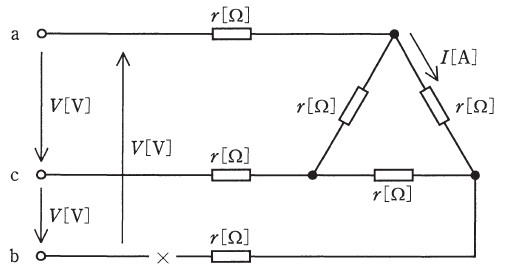
(a) 図中の電流Iの大きさ[A]は、断線前の何倍となるか。その倍率として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.50
- 0.58
- 0.87
- 1.15
- 1.73
(b) ×印の両側に現れる電圧の大きさ[V]は、電源の線間電圧の大きさV[V]の何倍となるか。その倍率として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0
- 0.58
- 0.87
- 1.00
- 1.15
解 説
(a)
断線前後の電流Iの比が問われているので、断線前と断線後のそれぞれの電流をVやrを用いて表し、その比を計算します。
まずは断線前から考えますが、問題文の図の1相あたりの等価回路は以下のようになります。1相あたりの等価回路は仮想中性線を用いるため、問題文のΔ結線はY結線に変換する必要がありますが、Δ→Yの変換の際には抵抗rは1/3倍されます。
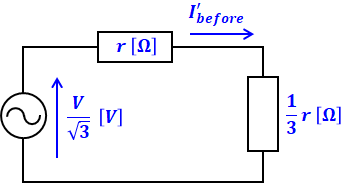
上図から、この等価回路を流れる電流I’beforeは、
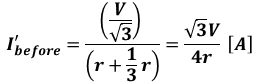
となりますが、求めたい電流Ibeforeは、問題の図にある通りΔ結線を流れる電流なので、I’beforeの1/√3倍の大きさになります。よって、Ibeforeは次のように計算することができます。
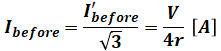
一方、断線後は三相回路が崩れ、ただの単相回路となるため、問題の回路図をそのまま使って計算することもできますが、わかりやすく描き直すと次のようになります。
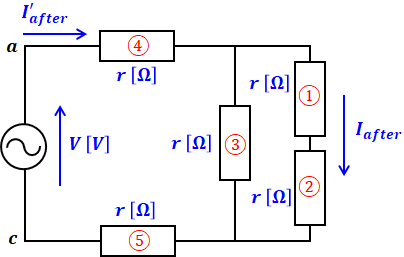
ここで求めたいのはIafterですが、そのためには、まず全ての抵抗を合成して、この回路全体を流れる電流I’afterを算出します。
合成抵抗をRとすると、まずは上図の抵抗(1)と抵抗(2)の2つの直列抵抗を合成し、その後それと抵抗(3)で並列の合成を行い、最後にそれと抵抗(4)と抵抗(5)の3つの直列抵抗の合成することでRが求められます。
![]()
![]()
![]()
よって、I’afterは以下のように求めることができます。
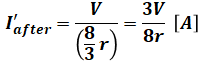
また、Iafterは、I’afterが抵抗(1)+(2)と抵抗(3)に分岐した前者を流れる電流であり、その電流値は抵抗比2:1の逆の関係になるので、
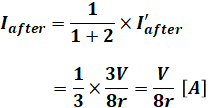
となります。
以上から、断線前後の電流比は、次のように計算することができます。
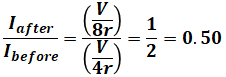
(b)
×印の両端の電圧差を求める必要がありますが、×印近辺は断線により電流が流れていないので、問題の図において×印のすぐ隣の抵抗は意味を持ちません(ただの電線と同じ扱いです)。よって、×印の両端の電圧差とは、下図の赤丸と青丸の間の電圧差と同等です。
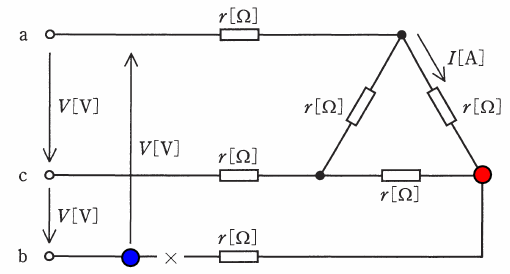
上図の回路において、aとbとcの電圧はそれぞれ120°ずつ異なる方向を向いたベクトルで表すことができ、一方、赤丸の箇所はaとcのちょうど中心に位置していることがわかります。よって、上図の回路のa、b、c、赤丸、青丸を電圧の向きを意識しながら図示すると、次のようになります。
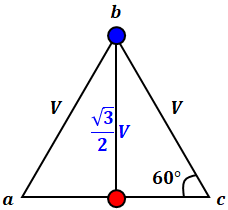
上図より、正三角形の一辺は線間電圧に相当するのでVで、赤丸と青丸の線分は正三角形の三角比より√3/2Vとなるため、求める答えは以下のように計算できます。
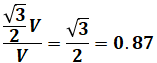

コメント