問 題
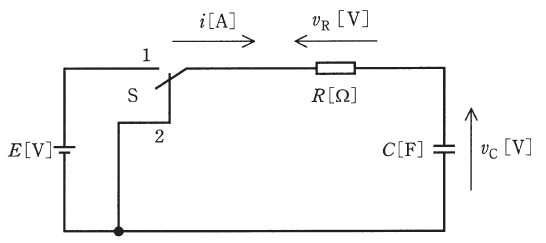
図のように、電圧E[V]の直流電源、スイッチS、R[Ω]の抵抗及び静電容量C[F]のコンデンサからなる回路がある。この回路において、スイッチSを1側に接続してコンデンサを十分に充電した後、時刻t=0sで、スイッチSを1側から2側に切り換えた。
2側に切り換えた以降の記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、自然対数の底は、2.718とする。
- 回路の時定数は、Cの値[F]に比例する。
- コンデンサの端子電圧vC[V]は、Rの値[Ω]が大きいほど緩やかに減少する。
- 時刻t=0sから回路の時定数だけ時間が経過すると、コンデンサの端子電圧vC[V]は直流電源の電圧E[V]の0.368倍に減少する。
- 抵抗の端子電圧vR[V]の極性は、切り換え前(コンデンサ充電中)と逆になる。
- 時刻t=0sにおける回路の電流i[A]は、Cの値[F]に関係する。
解 説
(1)に関して、RC直列回路における時定数Tの式は、
![]()
と表すことができるので、この記述は正しいです。
(2)で、(1)の解説の通り、Rが大きいと時定数Tも大きくなります。Tが大きければそれだけ定常状態(コンデンサに蓄えられたエネルギーを放出しきる)までの時間が長くなるということなので、vcの減少は緩やかになります。よって、これも正しい記述です。
(3)について、スイッチSを1側にして充分に時間が経つと、コンデンサの端子電圧vCは電源電圧Eと等しくなります。その後、スイッチを2側にすることで蓄えられたエネルギーが徐々に消費されるので、vCも時間とともに減少します。
このような充電と放電に関して、時間tとコンデンサの端子電圧vcの関係をグラフにすると、次のようになります。
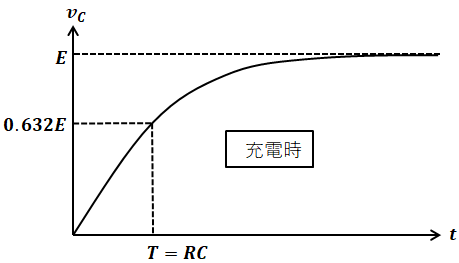
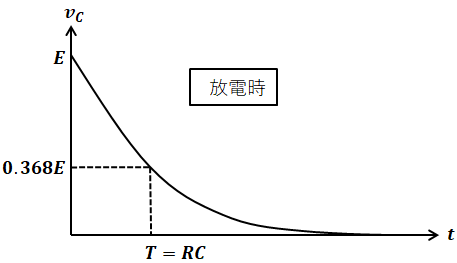
上記に記入してある通り、Eの63.2%分だけ充電するのに掛かる時間が時定数Tです。また、放電の際に、63.2%分だけ消費するのに掛かる時間も同じく時定数Tとなります。
よって、(3)のようにvC=Eの状態から時定数の時間が経過すると、63.2%失って36.8%残るため、これも正しい記述といえます。
(4)で、充電時は直流電源から電流が流れ出るので、問題の図の回路を時計回りに電流が流れます。一方、放電時はコンデンサから抵抗へと反時計回りに電流が流れるので、vRの極性は逆転します。よって、これも正しい記述です。
(5)に関して、コンデンサにエネルギーが充分に蓄えられてからスイッチを切り替えているので、t=0のときのコンデンサの端子電圧vCは、電源電圧Eと同じ大きさです(上図の放電時の図におけるt=0のところ参照)。
よって、放電を初めた瞬間だけはこのコンデンサは直流電源と同じ挙動を見せるため、電流iはCの値に関係なく、EをRで除した値となります。
このように考えて答えを(5)として構わないと思いますが、もう少し厳密に考えるなら、RC直列回路を流れる電流は以下の式で表されるので、
![]()
今回のようにt=0だと、
![]()
となって、iはEとRだけで決まるということがわかります。
以上から、(5)の記述が誤りなので、正解は(5)となります。

コメント