電験三種 H28年 機械 問15 問題と解説

　問 題　　　　　

定格出力3300kV・A、定格電圧6600V、定格力率0.9(遅れ)の非突極形三相同期発電機があり、星形接続1相当たりの同期リアクタンスは12.0Ωである。電機子の巻線抵抗及び磁気回路の飽和は無視できるものとして、次の(a)及び(b)の問に答えよ。

(a)　定格運転時における1相当たりの内部誘導起電力の値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3460
2. 3810
3. 6170
4. 7090
5. 8690

(b)　上記の発電機の励磁を定格状態に保ったまま運転し、星形結線1相当たりのインピーダンスが13+j5Ωの平衡三相誘導性負荷を接続した。このときの発電機端子電圧の値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3810
2. 4010
3. 5990
4. 6600
5. 6950

 

 

 

 

 

　解 説　　　　

(a)

まず、定格運転時の出力と電圧が問題文で与えられているので、定格電流は以下のように計算できます。

ここで、同期発電機の1相あたりの等価回路を以下に示します。

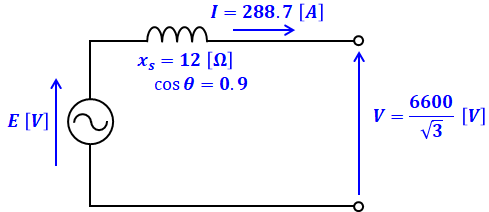
上図より、1相あたりの内部誘導起電力Eは、端子電圧Vに電圧降下分のIx_sを加えたものになりますが、力率を考慮したベクトル図を描くと、次のようになります。

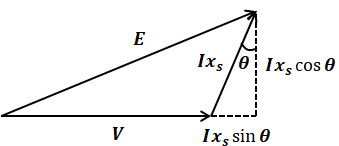
よって、Eは以下のように計算することができます。

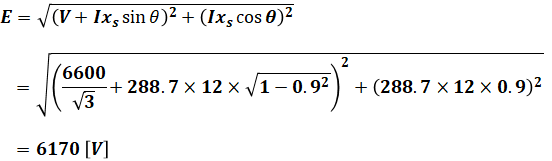
(b)

(b)では(a)の等価回路に負荷を接続しているので、その等価回路は次のように描くことができます。負荷の接続によって、回路を流れる電流I’や負荷の両端の電圧差V’の値は先ほどと変わってきますが、電源電圧Eはそのままです。

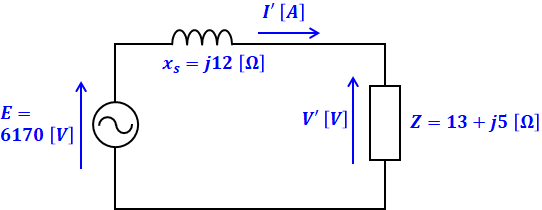
問われているのは発電機端子電圧の値なので、1相あたりの端子電圧(上図のV’)を√3倍したものが答えです。よって、当面の目標はV’を求めることですが、そのため、まずはI’を計算します。

回路全体のインピーダンスZ’は直列に並んだx_sとZとを合成すればよいので、次のようになります。

よって、回路を流れる電流I’は以下の計算により算出されます。

これで負荷のインピーダンスZと、そこを流れる電流I’がわかったので、その端子電圧V’は次のように計算できます。

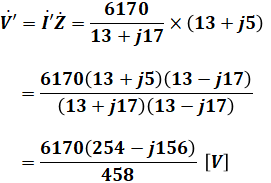
以上から、求める発電機端子電圧は、上記の1相分を三相回路全体に戻すために√3倍すればよいので、

となります。